在实际应用当中,对于数据较大的输入,归并排序是比较快的一个算法。该算法采用的是分治法的思想。本文会详细介绍归并排序的思想,并在文章后面加以实现。
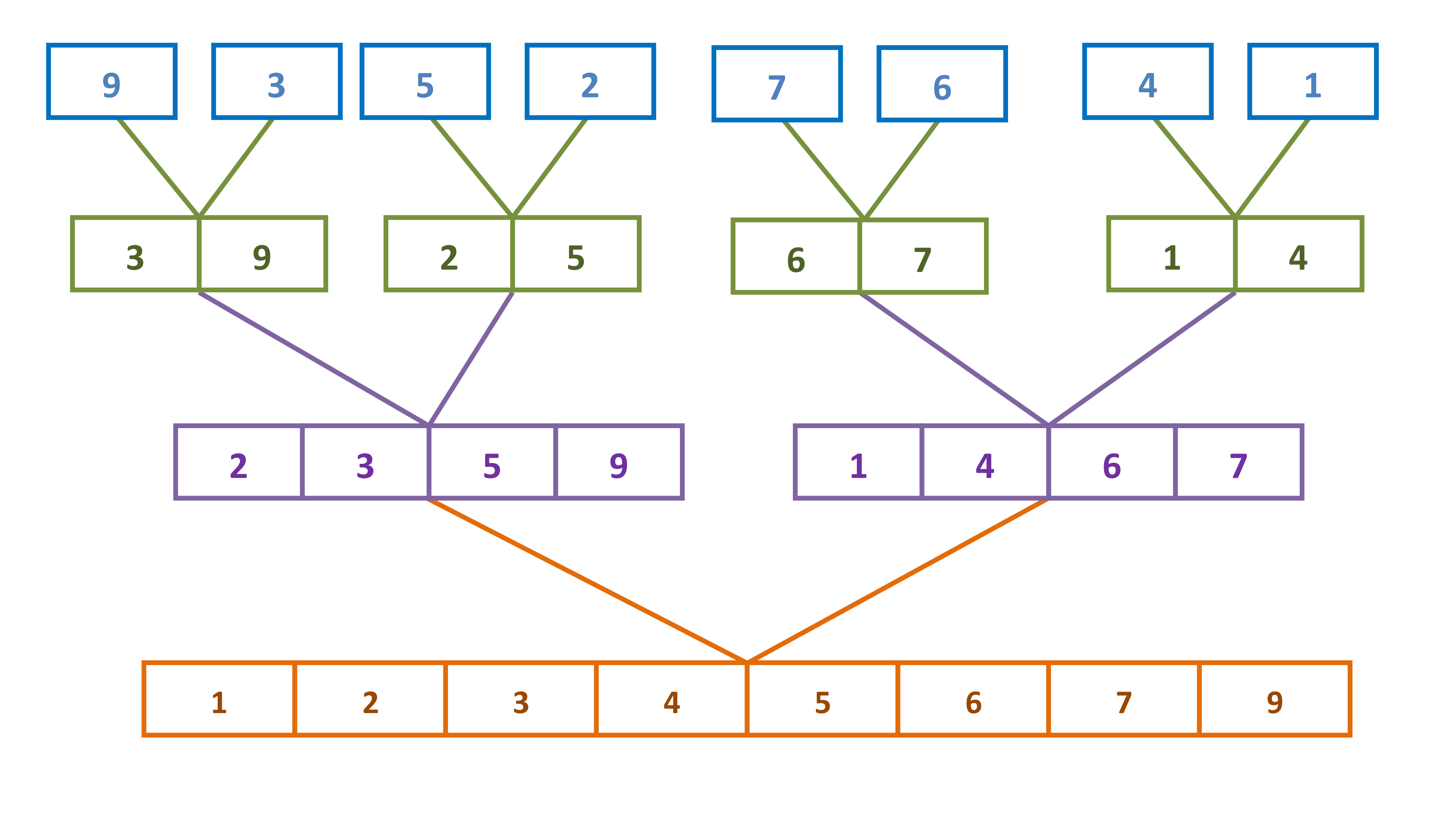
原理 :将数据分开排序,然后进行合并,最后形成一个排好的序列。
将其合并输出,如下图所示:
归并排序有一个关键步骤:合并两个排序好的序列。方法是:两个序列中的数相互比较,将较小的数先插入新的序列中。
归并过程:比较a[i]和a[j]的大小,若a[i]≤a[j],则将第一个有序表中的元素a[i]复制到r[k]中,并令i和k分别加上1;否则将第二个有序表中的元素a[j]复制到r[k]中,并令j和k分别加上1,如此循环下去,直到其中一个有序表取完,然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现,先把待排序区间[s,t]以中点二分,接着把左边子区间排序,再把右边子区间排序,最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。
发明者:约翰·冯·诺伊曼
时间复杂度:O(nlogn)
空间复杂度 O(n)
稳定的算法
一次合并 在代码实现部分,需要进行递归进行合并,因此,先编写一个合并的方法。
归并操作的工作原理如下:
一次归并函数传递的参数有:一个数组名、数组的起始位置、数组的末尾位置以及数组的中点位置。
第一步:申请空间,初始化起点中点和中点到末尾位置两个变量(nl,nr),同时设定两个指针p和q,空间大小分别为nl和nr;
第二步:将数组分别输入到两个空间中;
第三步:合并两个数组。操作:比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
重复步骤3直到某一指针超出序列尾;
将另一序列剩下的所有元素直接复制到合并序列尾.
在第三步的时候,需要注意的是,不额外的开辟辅助数组,直接通过两个指针的值将原数组的数值进行修改。此处需要设置一个变量k,起始位置为数组的起始位置,方便在合并时同时增加指针的下标和数组下标值.
注:使用malloc时,需要引入#include <stdlib.h>头文件。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 void mergeOne(int nums[], int l, int m , int r){ int nl = m - l + 1 ; int nr = r - m ; int *p = NULL, *q = NULL; p = (int *) malloc (nl * sizeof(int )); q = (int *) malloc (nr * sizeof(int )); //将数组输入到两个空间中 for (int i = 0 ; i < nl; i++) { p[i] = nums[l + i]; } for (int j = 0 ; j < nr; j++) { q[j] = nums[m + 1 + j]; } //合并两个数组 int i = 0 ; int j = 0 ; int k = l; while (i < nl && j < nr) { if (p[i] < q[j] ) { nums[k++] = p[i++]; }else { nums[k++] = q[j++] ; } } //将剩余的元素合并 while (i < nl) { nums[k++] = p[i++]; } while (j <nr) { nums[k++] = q[j++] ; } }
归并排序 通过合并函数来实现归并排序的算法
1 2 3 4 5 6 7 8 9 //注意:此处的left 和right 必须是数组下标能取到的有效值 void mergeSort(int nums[], int left , int right ) { int mid = (left + right ) >> 1 ; if (left < right ) { mergeSort(nums, left , mid ); mergeSort(nums, mid +1 , right ); mergeOne(nums, left , mid , right ); } }
测试 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 #include <iostream> #include <stdlib.h> void print_array (int nums[], int n) using namespace std ;int main () int nums[]={9 , 3 , 5 , 2 , 7 , 6 , 4 , 1 }; int n = sizeof (nums)/sizeof (nums[0 ]); mergeSort(nums, 0 , n - 1 ); print_array(nums,n); return 0 ; } void print_array (int nums[], int n) for (int i = 0 ; i<n; i++){ cout <<nums[i]<<" " ; } cout <<endl ; }
最后输出:
1 2 3 4 5 6 7 9
Process returned 0 (0x0) execution time : 0.097 s
Press any key to continue.