Machine Learning algorithm - Adaboost

Posted on   |   In   |     |   views

Github源码实现：https://github.com/csuldw/MachineLearning/tree/master/Adaboost

本文主要介绍的是Adaboost算法，利用AdaBoost元算法来提高分类器的性能，主要参考《机器学习实战》来学习Adaboost，同时结合Wikipedia以及各位同道人士的经验等，希望可以通过总结达到学习效果。

基于数据集多重抽样的分类器

先来看看Adaboost的优缺点。

Feature AdaBoost
优点 泛化错误率低，易编码，可以应用在大部分分类器上，无需参数调整
缺点 对离群点敏感
数据 数值型和标称型数据

下面，来看看bagging和boosting的不同：

  • bagging: 一种基于数据随机重抽样的分类器构建方法。自举汇聚法(bootstrap aggregating),也叫做bagging方法，是从原始数据集选择$S$次（有放回的抽取）后得到$S$个新数据集的一种技术。新数据集和原始数据集的大小相等（维数和列数都相等）。每个数据集都是通过在原始数据集中随机选择一个来进行替换而得到的。在S个数据集建好之后，将某个机器学习算法分别作用域每个数据集就可以得到S个分类器。当我们对新数据进行分类时，就可以应用S个分类器进行分类。与此同时，选择分类器投票结果最多的类别作为最后的分类结果。目前，有一种改进的bagging方法，如随机森林（RF,随机森林不同的是，它对列也进行采样），它在一定程度上可以防止过拟合，也是对决策树的一种改进。

  • boosting则是一种与bagging很类似的技术。不论是boosting还是bagging当中，使用的多个分类器的类型都是一致的。但是在前者当中，不同的分类器是通过串行训练而得到，每个新分类器都根据已训练出的分类器的性能来进行训练。boosting则是通过训练集中关注被已有分类器错分的那些数据来获得新的分类器。

boosting方法有多个版本，当前最流行便是AdaBoost。Adaboost 学习的一般流程如下：

1
2
3
4
5
6
收集数据：可以使用任何方法；  
准备数据：依赖于所使用的弱分类器类型；  
分析数据：可以使用任意方法  
训练算法：AdaBoost的大部分时间都用在训练上，分类器将多次在同一数据集上训练弱分类器；  
测试算法：计算分类的错误率；  
使用算法：同SVM一样，AdaBoost预测的两个类别中的一个，如果是多类，也可使用与SVM一样的方法。

训练算法：基于错误率提升分类器性能

AdaBoost是adaptive boosting（自适应 boosting）的缩写，其运行过程如下：

训练集中的每个样本，赋予其一个权重，这些权重构成向量$D$。一开始，这些权重都初试化成相等值$\frac{1}{N}$，其中$N$为样本个数。首先在训练数据上训练出一个弱分类器并计算该分类器的错误率，然后在同一数据集上再次训练弱分类器。接着，在分类器的第二次训练当中，将会重新调整每个样本的weight，其中第一次正确分类的样本的weight将会降低，而第一次错误分类的样本的weight将会提高。为了从所有分类器中得到最终的分类结果，AdaBoost会为每个分类器都赋予一个权重值$\alpha$，这些$\alpha$则是基于每个分类器的错误率进行计算的。

在模型训练时，错误率定义为：

$$\epsilon=\dfrac{未正确分类的样本数目}{所有样本数目}$$

系数$\alpha$的计算公式为:

$$\alpha=\dfrac{1}{2}ln(\dfrac{1-\epsilon}{\epsilon})$$

从上面两个式子可以看出，$\alpha$和$\epsilon$是成反比的，$\epsilon$越大，$\alpha$就越小，也就是说建立的这个模型应该赋予更少的weight。计算出$\alpha$值之后，可以对weight向量$D$进行更新，使得正确分类的样本weight降低而错分类的样本weight值升高，$D$的计算方法如下
如果某个样本被正确分类，更新该样本权重值为：

$$D^{(t+1)}_i=\dfrac{D_i^{(t)} e^{-\alpha}}{Sum(D)}$$

如果某个样本被错误分类，更新该样本的权重值为：

$$D^{(t+1)}_i=\dfrac{D_i^{(t)} e^{\alpha}}{Sum(D)}$$

计算出$D$后，AdaBoost会继续下一轮迭代，不断地重复训练和调整weight的过程，直到训练error ratio为0或者weak classifier的数目达到用户指定的特定值为止。Adaboost算法也是一种加和模型，最终的到的classifier可以表示成如下形式：

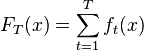
在建立完整的AdaBoost算法之前，需要通过一些代码建立weak classifier并保存数据集的weight。

基于单层决策树构建弱分类器

单层决策树是一种简单的决策树。首先构建一个简单的数据集,建立一个adaboost.py文件并加入下列代码：

1
2
3
4
5
6
7
8
def loadSimpData():
    datMat = matrix([[ 1. ,  2.1],
        [ 2. ,  1.1],
        [ 1.3,  1. ],
        [ 1. ,  1. ],
        [ 2. ,  1. ]])
    classLabels = [1.0, 1.0, -1.0, -1.0, 1.0]
    return datMat,classLabels

导入数据

1
2
>>> import adaboost
>>> datMat,classLabels=adaboost.loadSimpData()

下面两个函数，一个用于测试是否某个值小于或者大于我们正在测试的阈值，一个会在一个加权数据集中循环，并找到具有最低错误率的单层决策树。

伪代码如下：

将最小错误率minError设为无穷大
对数据及中的每一个特征（第一层循环）：
    对每个步长（第二层循环）：
        对每个不等号（第三层循环）：
            建立一颗单层决策树并利用加权数据集对它进行测试
            如果错误率低于minError，则将当前单层决策树设置为最佳单层决策树
返回最佳单层决策树

单层决策树生成函数代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data
    retArray = ones((shape(dataMatrix)[0],1))
    if threshIneq == 'lt':
        retArray[dataMatrix[:,dimen] <= threshVal] = -1.0
    else:
        retArray[dataMatrix[:,dimen] > threshVal] = -1.0
    return retArray
    

def buildStump(dataArr,classLabels,D):
    dataMatrix = mat(dataArr); labelMat = mat(classLabels).T
    m,n = shape(dataMatrix)
    numSteps = 10.0; bestStump = {}; bestClasEst = mat(zeros((m,1)))
    minError = inf #init error sum, to +infinity
    for i in range(n):#loop over all dimensions
        rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max();
        stepSize = (rangeMax-rangeMin)/numSteps
        for j in range(-1,int(numSteps)+1):#loop over all range in current dimension
            for inequal in ['lt', 'gt']: #go over less than and greater than
                threshVal = (rangeMin + float(j) * stepSize)
                predictedVals = stumpClassify(dataMatrix,i,threshVal,inequal)#call stump classify with i, j, lessThan
                errArr = mat(ones((m,1)))
                errArr[predictedVals == labelMat] = 0
                weightedError = D.T*errArr  #calc total error multiplied by D
                #print "split: dim %d, thresh %.2f, thresh ineqal: %s, the weighted error is %.3f" % (i, threshVal, inequal, weightedError)
                if weightedError < minError:
                    minError = weightedError
                    bestClasEst = predictedVals.copy()
                    bestStump['dim'] = i
                    bestStump['thresh'] = threshVal
                    bestStump['ineq'] = inequal
    return bestStump,minError,bestClasEst

AdaBoost算法的实现

整个实现的伪代码如下：

对每次迭代：
    利用buildStump()函数找到最佳的单层决策树
    将最佳单层决策树加入到单层决策树数据中
    计算alpha
    计算心的权重向量D
    更新累计类别估计值
    如果错误率低于0.0 则退出循环

基于单层决策树的AdaBoost训练过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def adaBoostTrainDS(dataArr,classLabels,numIt=40):
    weakClassArr = []
    m = shape(dataArr)[0]
    D = mat(ones((m,1))/m)   #init D to all equal
    aggClassEst = mat(zeros((m,1)))
    for i in range(numIt):
        bestStump,error,classEst = buildStump(dataArr,classLabels,D)#build Stump
        #print "D:",D.T
        alpha = float(0.5*log((1.0-error)/max(error,1e-16)))#calc alpha, throw in max(error,eps) to account for error=0
        bestStump['alpha'] = alpha  
        weakClassArr.append(bestStump)                  #store Stump Params in Array
        #print "classEst: ",classEst.T
        expon = multiply(-1*alpha*mat(classLabels).T,classEst) #exponent for D calc, getting messy
        D = multiply(D,exp(expon))                              #Calc New D for next iteration
        D = D/D.sum()
        #calc training error of all classifiers, if this is 0 quit for loop early (use break)
        aggClassEst += alpha*classEst
        #print "aggClassEst: ",aggClassEst.T
        aggErrors = multiply(sign(aggClassEst) != mat(classLabels).T,ones((m,1)))
        errorRate = aggErrors.sum()/m
        print "total error: ",errorRate
        if errorRate == 0.0: break
    return weakClassArr,aggClassEst

测试

拥有了多个弱分类器以及其对应的$alpha$值，进行测试就方便了。

AdaBoost分类函数:利用训练处的多个弱分类器进行分类的函数。

1
2
3
4
5
6
7
8
9
10
11
def adaClassify(datToClass,classifierArr):
    dataMatrix = mat(datToClass)#do stuff similar to last aggClassEst in adaBoostTrainDS
    m = shape(dataMatrix)[0]
    aggClassEst = mat(zeros((m,1)))
    for i in range(len(classifierArr)):
        classEst = stumpClassify(dataMatrix,classifierArr[i]['dim'],\
                                 classifierArr[i]['thresh'],\
                                 classifierArr[i]['ineq'])#call stump classify
        aggClassEst += classifierArr[i]['alpha']*classEst
        print aggClassEst
    return sign(aggClassEst)

OK，文章粗略地的讲解了下Adaboost，主要从实现中讲解，如果要知道原理，请看文献Wiki-AdaBoost，Wikipedia中讲解的比较清楚，由于能力有限，以后再回头补充吧。

References