此文是一篇译文,是本人于今年四月应CSDN编辑之邀翻译的一篇文章,原文发表于今年三月 [Escaping from Saddle Points](共两篇),此文是第一篇文章的译文,第二篇文章尚未翻译,如有需要请点击原文 Saddles Again。文章讲述了各式各样的 critical points 以及使用何种方法来来避开 saddle point(鞍点),个人觉得比较实用,属于纯理论知识,因此重新整理了一番,受益匪浅。详细内容请看正文。
凸函数比较简单——它们通常只有一个局部最小值。非凸函数则更加复杂。在这篇文章中,我们将讨论不同类型的临界点(critical points),当你在寻找凸路径(convex path)的时候可能会遇到。特别是,基于梯度下降的简单启发式学习方法,在很多情形下会致使你在多项式时间内陷入局部最小值(local minimum)。
不同类型的 Critical Points
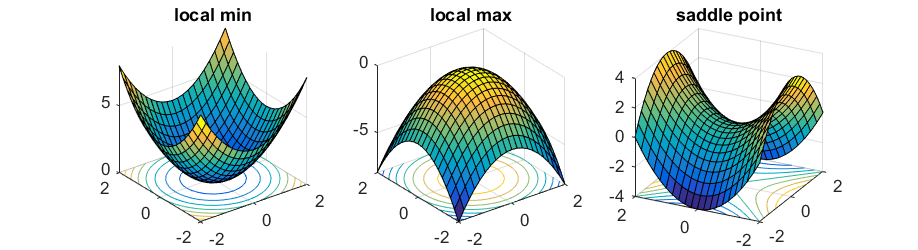
为了最小化函数$f:\mathbb{R}^n\to \mathbb{R}$,最流行的方法就是往负梯度方向前进$\nabla f(x)$(为了简便起见,我们假定谈及的所有函数都是可微的),即:
$$y = x - \eta \nabla f(x),$$
其中η表示步长。这就是梯度下降算法(gradient descent algorithm)。
每当梯度$\nabla f(x)$不等于零的时候,只要我们选择一个足够小的步长η,算法就可以保证目标函数向局部最优解前进。当梯度$\nabla f(x)$等于$\vec{0}$时,该点称为临界点(critical point),此时梯度下降算法就会陷入局部最优解。对于(强)凸函数,它只有一个临界点(critical point),也是全局最小值点(global minimum)。
然而,对于非凸函数,仅仅考虑梯度等于$\vec{0}$远远不够。来看一个简单的实例:
$$ y= x1^2 −x2^2 $$
当$x=(0,0)$时,梯度为 $\vec{0}$,很明显此点并不是局部最小值点,因为当$x = (0, \epsilon)$时函数值更小。在这种情况下,(0,0)点叫作该函数的鞍点(saddle point )。
为了区分这种情况,我们需要考虑二阶导数$\nabla^2 f(x)$——一个$n×n$的矩阵(通常称作Hessian矩阵),第i,j项等于$\frac{\partial ^2}{\partial x_1 x_2} f(x)$ 。当Hessian矩阵正定时(即对任意的$u≠0$,有$u^⊤ ∇^2 f(x)u > 0$恒成立),对于任何方向向量$u$,通过二阶泰勒展开式$f(x + \eta u) \approx f(x) + \frac{\eta^2}{2} u^\top\nabla^2 f(x) u > f(x),$ ,可知$x$必定是一个局部最小值点。同样,当Hessian矩阵负定时,此点是一个局部最大值点;当Hessian矩阵同时具有正负特征值时,此点便是鞍点。
对于许多问题,包括learning deep nets,几乎所有的局部最优解都有与全局最优解(global optimum)非常相似的函数值,因此能够找到一个局部最小值就足够好了。然而,寻找一个局部最小值也属于NP-hard问题(参见Anandkumar,GE 2006中的讨论一节)。实践当中,许多流行的优化技术都是基于一阶导的优化算法:它们只观察梯度信息,并没有明确计算Hessian矩阵。这样的算法可能会陷入鞍点之中。
在文章的剩下部分,我们首先会介绍,收敛于鞍点的可能性是很大的,因为大多数自然目标函数都有指数级的鞍点。然后,我们会讨论如何对算法进行优化,让它能够尝试去避开鞍点。
在文章的剩下部分,我们首先会介绍,收敛于鞍点的可能性是很大的,因为大多数自然目标函数都有指数级的鞍点。然后,我们会讨论如何对算法进行优化,让它能够尝试去避开鞍点。
对称与鞍点(Symmetry and Saddle Points)
许多学习问题都可以被抽象为寻找$k$个不同的分量(比如特征,中心…)。例如,在聚类问题中,有$n$个点,我们想要寻找$k$个簇,使得各个点到离它们最近的簇的距离之和最小。又如在一个两层的神经网络中,我们试图在中间层寻找一个含有$k$个不同神经元的网络。在我先前的文章中谈到过张量分解(tensor decomposition),其本质上也是寻找$k$个不同的秩为1的分量。
解决此类问题的一种流行方法是设计一个目标函数:设$x_1, x_2, \ldots, x_k \in \mathbb{R}^n$表示所求的中心(centers ),让目标函数$f(x_1,…,x_k)$来衡量函数解的可行性。当向量$x_1,x_2,…,x_k$是我们需要的$k$的分量时,此函数值会达到最小。
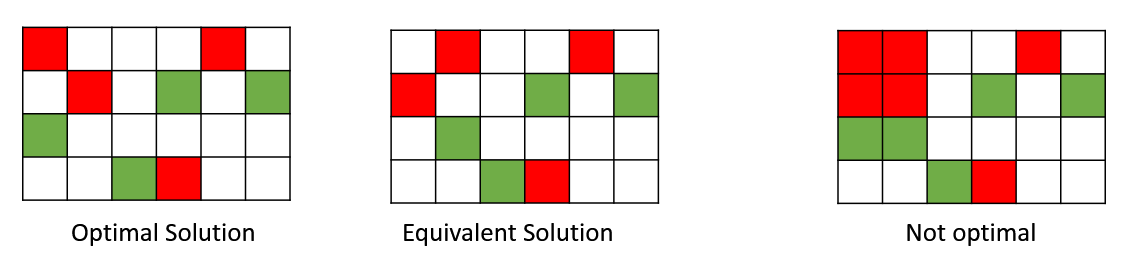
这种问题在本质上是非凸的自然原因是转置对称性(permutation symmetry)。例如,如果我们将第一个和第二个分量的顺序交换,目标函数相当于:$f(x_1,x_2,…,x_k) = f(x_2, x_1,…,x_k)$.
然而,如果我们取平均值,我们需要求解的是$\frac{x_1+x_2}{2}, \frac{x_1+x_2}{2}, x_3,…,x_k$,两者是不等价的!如果原来的解是最优解,这种均值情况很可能不是最优。因此,这种目标函数不是凸函数,因为对于凸函数而言,最优解的均值仍然是最优。
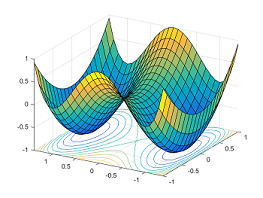
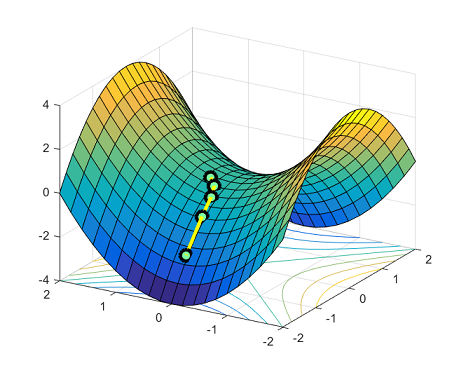
所有相似解的排列有指数级的全局最优解。鞍点自然会在连接这些孤立的局部最小值点上出现。下面的图展示了函数$y = x_1^4-2x_1^2 + x_2^2$:在两个对称的局部最小点$(−1,0)$和$(1,0)$之间,点$(0,0)$是一个鞍点。
避开鞍点(Escaping from Saddle Points)
为了优化这些存在许多鞍点的非凸函数,优化算法在鞍点处(或者附近)也需要向最优解前进。最简单的方法就是使用二阶泰勒展开式:
$$f(y) \approx f(x) + \left<\nabla f(x), y-x\right>+\frac{1}{2} (y-x)^\top \nabla^2 f(x) (y-x).$$
如果$\nabla f(x)$的梯度为$\vec{0}$,我们仍然希望能够找到一个向量$u$,使得$u^\top \nabla^2 f(x) u < 0$。在这种方式下,如果我们令$y = x+\eta u$,函数值$f(y)$就会更小。许多优化算法,诸如 trust region algorithms 和 cubic regularization使用的就是这种思想,它们可以在多项式时间内避开鞍点。
严格鞍函数(Strict Saddle Functions)
通常寻找局部最小值也属于NP-hard问题, 许多算法都可能陷入鞍点之中。那么避开一个鞍点需要多少步呢?这与鞍点的表现良好性密切相关。直观地说,如果存在一个方向$u$,使得二阶导$u^\top \nabla^2 f(x) u$明显比0小,则此鞍点x表现良好(well-behaved)——从几何上来讲,它表示存在一个陡坡方向会使函数值减小。为了量化它,在我与Furong Huang, Chi Jin and Yang Yuan合作的一篇论文中 介绍了严鞍函数的概念(在Sun et al. 2015一文中称作“ridable”函数)
对于所有的$x$,如果同时满足下列条件之一,则函数$f(x)$是严格鞍函数:
- 梯度$\nabla f(x)$很大。
- Hessian矩阵$\nabla^2 f(x)$具有负的特征值。
- 点$x$位于局部极小值附近。
从本质上讲,每个点x的局部区域看起来会与下图之一类似:
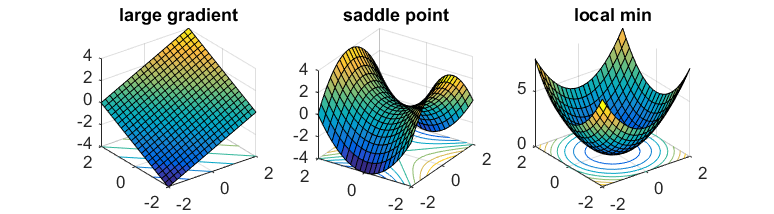
对于这种函数,trust region算法 和 cubic regularization 都可以有效地找到一个局部最小值点。
定理(非正式):至少存在一种多项式时间算法,它可以找到严格鞍函数的局部最小值点。
什么函数是严格鞍? Ge et al. 2015 表明张量分解(tensor decomposition)问题属于严格鞍。 Sun et al. 2015观察到诸如完整的dictionary learning,phase retrieval 问题也是严格鞍。
定理(非正式):至少存在一种多项式时间算法,它可以找到严格鞍函数的局部最小值点。
一阶方法避开鞍点(First Order Method to Escape from Saddle Points)
Trust region算法非常强大。然而它们需要计算目标函数的二阶导数,这在实践中往往过于费时。如果算法只计算函数梯度,是否仍有可能避开鞍点?
这似乎很困难,因为在鞍点处梯度为$\vec{0}$,并且没有给我们提供任何信息。然而,关键在于鞍点本身是非常不稳定的(unstable):如果我们把一个球放在鞍点处,然后轻微地抖动,球就可能会掉下去!当然,我们需要让这种直觉在更高维空间形式化,因为简单地寻找下跌方向,需要计算Hessian矩阵的最小特征向量。
为了形式化这种直觉,我们将尝试使用一个带有噪声的梯度下降法(noisy gradient descent)
$$y = x - \eta \nabla f(x) + \epsilon.$$
这里$\epsilon$是均值为$0$的噪声向量。这种额外的噪声会提供初步的推动,使得球会顺着斜坡滚落。
事实上,计算噪声梯度通常比计算真正的梯度更加省时——这也是随机梯度法(stochastic gradient )的核心思想,大量的工作表明,噪声并不会干扰凸优化的收敛。对于非凸优化,人们直观地认为,固有的噪声有助于收敛,因为它有助于当前点远离鞍点( saddle points)。这并不是bug,而是一大特色!
多项式高度依赖于维度N和Hessian矩阵的最小特征值,因此不是很实用。对于严格鞍问题,找到最佳收敛率仍是一个悬而未决的问题。
最近 Lee et al.的论文表明如果初始点是随机选择的,那么即使没有添加噪声,梯度下降也不会收敛到任何严格鞍点。然而他们的结果依赖于动态系统理论(dynamical systems theory)的稳定流形定理(Stable Manifold Theorem),其本身并不提供任何步数的上界。
复杂鞍点
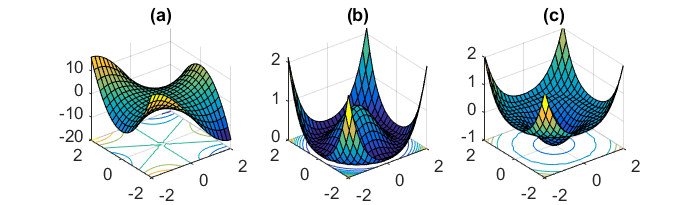
通过上文的介绍,我们知道算法可以处理(简单)的鞍点。然而,非凸问题的外形更加复杂,含有退化鞍点(degenerate saddle points )——Hessian矩阵是半正定的,有$0$特征值。这样的退化结构往往展示了一个更为复杂的鞍点(如monkey saddle(猴鞍),图(a))或一系列连接的鞍点(图(b)(c))。在Anandkumar, Ge 2016我们给出了一种算法,可以处理这些退化的鞍点。
非凸函数的轮廓更加复杂,而且还存在许多公认的问题。还有什么函数是严格鞍?当存在退化鞍点,或者有伪局部最小值点时,我们又该如何使优化算法工作呢?我们希望有更多的研究者对这类问题感兴趣!
如有时间,可继续看看下一篇文章(英文):Saddles Again.