神经网络之激活函数

Posted on   |   In   |     |   views

在神经网络里面，会经常用到activation function，不管是CNN还是RNN亦或是其他带有神经元的网络，activation function都扮演着重要角色。刚接触神经网络的时候，脑子里总会浮现很多问题。为什么会有这么多activation function?为何这个函数就比另一个效果好？这么多函数，我们该使用哪一个？出于学习目的，本文将对activation function进行简要的归纳，旨在屡清各个函数的应用场景。

前言介绍

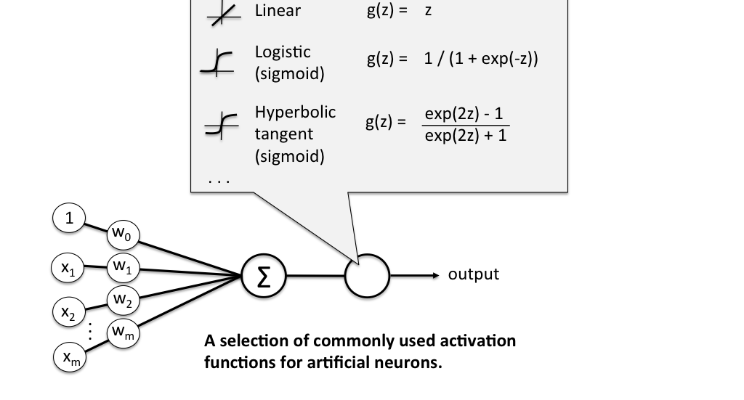
一个神经网络包含很多的神经元，每个神经元上都伴随着一个Activation Function，而神经元将Activation Function的值作为其输出（同时作为下一层的输入）。Activation Function译名叫做激活函数，通常将其划分为线性激活函数（linear Activation Function）和非线性激活函数（Non-linear Activation Function）。一般情况下，如果神经网络中使用的是linear Activation Function，那么每一层都相当于是上一层的线性组合，其输入和输出均是线性的，此时就类似于感知机模型，那么hidden layer就没有存在的意义了，同时这种线性函数对于复杂的非线性问题拟合效果欠缺。当我们使用非线性激活函数时，模型可以拟合任意函数的输出，表现空间更大、使用范围更广、且效果更佳。

激活函数的类型特别多，本文主要介绍下面几个常用的非线性激活函数：

  1. sigmoid
  2. tanh（Hyperbolic tangent）
  3. ReLU (Rectified Linear Unit)
  4. Leaky ReLU

下面根据激活函数的演进来看看各大激活函数的优缺点。

Sigmoid Activation Function

sigmoid函数是一个有界可导的实函数，同时sigmoid函数还是单调的，其表达式如下：

$$
\sigma(x) = \frac{1}{1+e^{-x}}
\label{1}\tag{1}
$$

根据表达式，我们可以使用Python绘制出sigmoid曲线：

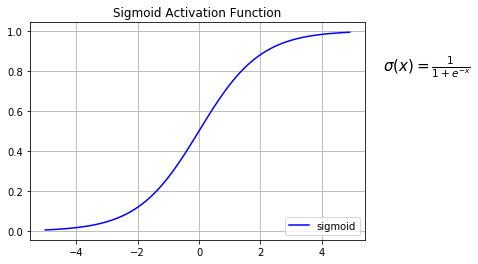
从上图我们看出，sigmoid函数取值在0到1，因此我们一般使用sigmoid的值作为概率输出，如LR：

特点：

  1. 导数$\sigma’ = \sigma (1- \sigma)$
  2. sigmoid单调，导数非单调；
  3. 值域0到1之间，可表示概率。线性激活函数的值域在(-inf,+inf)，而sigmoid的值域在(0,1)，能够很好的表示概率。

缺点：在sigmoid的两端，X的变化对Y的作用不大，以致在训练过程中，位于这部分区间的数据点的梯度会特别小，甚至会产生Vanishing Gradient Problem，从而导致训练速度变慢，难以收敛。

绘制sigmoid曲线代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
import matplotlib.pyplot as plt
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))
x = np.arange(-5., 5., 0.1)
y_sig = sigmoid(x)
plt.plot(x, y_sig, 'b', label='sigmoid')
plt.grid()
plt.title("Sigmoid Activation Function")
plt.text(6, 0.8, r'$\sigma(x)=\frac{1}{1+e^{-x}}$', fontsize=15)
plt.legend(loc='lower right')
plt.show()

tanh Activation Function

tanh激活函数跟sigmoid激活函数的图像很像，只是抑制区域不一样。tanh也可以用sigmoid进行表示，如下：

$$
tanh(x) = \frac{1-e^{-2x}}{1+e^{-2x}}=2 \cdot sigmoid(2x)-1
\label{2}\tag{2}
$$

图型如下：

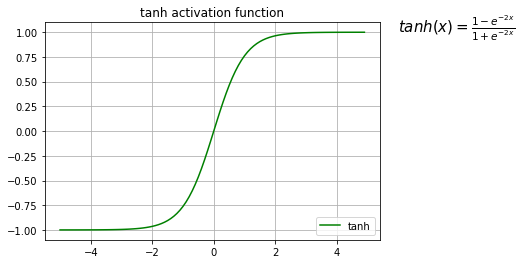
tanh函数特点：

  1. 导数为$tanh’(x) = 1- tanh^2(x)$
  2. tanh属于单调函数，但其导数非单调；
  3. 值域(-1,1)，以0为中心；

缺点：与sigmoid一样，同样会出现vanishing gradient problem。

绘制tanh曲线代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import matplotlib.pyplot as plt
import numpy as np

def tanh(x):
    return (1-np.exp(-2*x))/(1 + np.exp(-2*x))

x = np.arange(-5., 5., 0.1)
plt.grid()

plt.plot(x, tanh(x), 'g', label='tanh')
plt.title("tanh activation function")
plt.text(6,1, r'$tanh(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$', fontsize=15)
plt.legend(loc='lower right')
plt.show()

ReLU

ReLU函数也是非线性激活函数，它很好的避免了 vanishing gradient problem，不过在坐标轴的正侧，它是一个线性函数，表达式如下：

$$
ReLU(x) = max(0, x)
\label{3}\tag{3}
$$

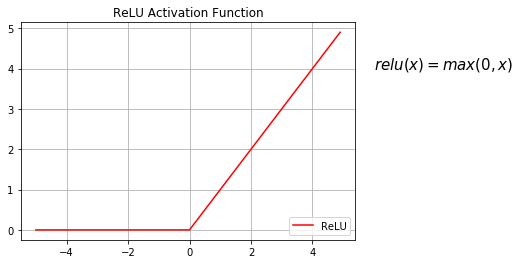
ReLU函数特点：

  1. 导数：当x<=0时，导数为0；当x>0时，导数为1；
  2. 任何函数都可以近似采用ReLU函数的组合进行表示；
  3. 取值[0, inf)，可以放大激活函数，但是负区域会完全的终止神经元的传输，因此出现了ReLU的变体Leaky ReLU等。
  4. 受限于hidden layer使用。

绘制ReLU曲线代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import matplotlib.pyplot as plt
import numpy as np

def relu(x):
    return np.maximum(0, x)

x = np.arange(-5., 5., 0.1)
y_relu = relu(x)
plt.plot(x, y_relu, 'r', label='ReLU')
plt.grid()
plt.title("ReLU Activation Function")
plt.text(6, 4, r'$relu(x)=max(0, x)$', fontsize=15)
plt.legend(loc='lower right')
plt.show()

Leaky ReLU

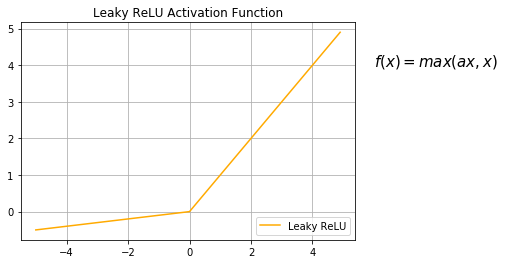
Leaky ReLU是ReLU的变体，目的是使得激活函数的梯度不为零，不仅可以抑制神经元，同时还可以恢复神经元的向后传递。表达式如下：

$$
f(x) = max(\alpha x, x)
\label{4}\tag{4}
$$

绘制Leaky ReLU曲线代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import matplotlib.pyplot as plt
import numpy as np

def leaky_relu(x, a=0.1):
    return np.maximum(a*x, x)

x = np.arange(-5., 5., 0.1)
y_relu = leaky_relu(x)
plt.plot(x, y_relu, '#FFAA00', label='Leaky ReLU')
plt.grid()
plt.title("Leaky ReLU Activation Function")
plt.text(6, 4, r'$f(x)=max(ax, x)$', fontsize=15)
plt.legend(loc='lower right')
plt.show()

扩展

https://en.wikipedia.org/wiki/Activation_function


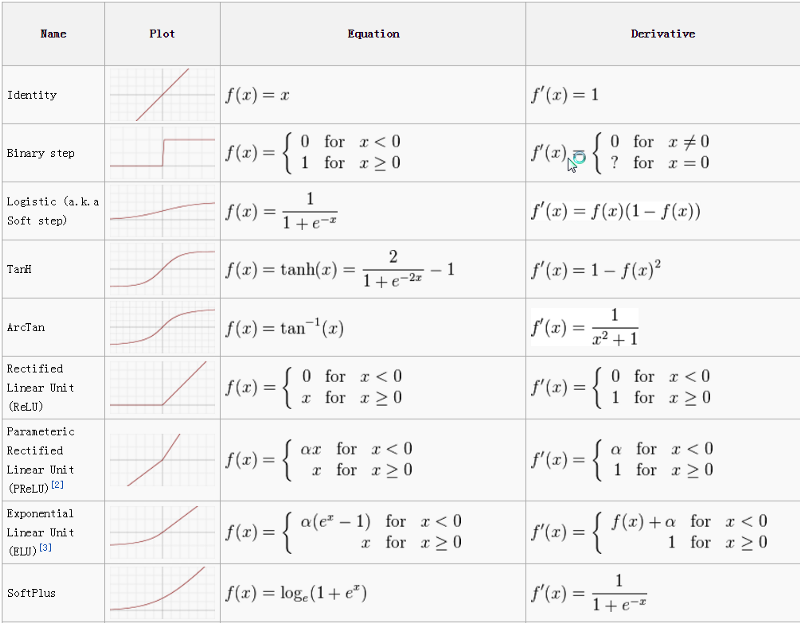
Fig: Activation Function Cheetsheet

总结

上面说到ReLU激活函数及其变体的效果很出色，但是是不是 全部都采用ReLU呢？当然不是，在处理分类任务是，sigmoid还是表现的相当出色的，并且解释性更强，更简单。如果你在训练神经网络模型的时候不知道采用何种激活函数，可以先采用ReLU和tanh进行训练，相信你肯定会得到一个不错的baseline。

References

  1. The equivalence of logistic regression and maximum entropy models
  2. The Origins of Logistic Regression - Tinbergen Institute
  3. Understanding Activation Functions in Neural Networks
  4. Activation functions and it’s types-Which is better?