机器学习算法-K-means聚类

Posted on   |   In   |     |   views

Github源码:https://github.com/csuldw/MachineLearning/tree/master/Kmeans

k-Means算法是一种聚类算法，它是一种无监督学习算法，目的是将相似的对象归到同一个蔟中。蔟内的对象越相似，聚类的效果就越好。聚类和分类最大的不同在于，分类的目标事先已知，而聚类则不一样。其产生的结果和分类相同，而只是类别没有预先定义。

算法原理

设计的目的：使各个样本与所在簇的质心的均值的误差平方和达到最小（这也是评价K-means算法最后聚类效果的评价标准）。

$$SSE = \sum_{i=1}^k \sum_{x \epsilon C_{i} } ||x-\mu_i||_{2}^2$$

K-均值聚类

  • 优点：容易实现
  • 缺点：可能收敛到局部最小值，在大规模数据上收敛较慢
  • 适合数据类型：数值型数据

步骤

  1. 创建k个点作为k个簇的起始质心（经常随机选择）。
  2. 分别计算剩下的元素到k个簇中心的相异度（距离），将这些元素分别划归到相异度最低的簇。
  3. 根据聚类结果，重新计算k个簇各自的中心，计算方法是取簇中所有元素各自维度的算术平均值。
  4. 将D中全部元素按照新的中心重新聚类。
  5. 重复第4步，直到聚类结果不再变化。
  6. 最后，输出聚类结果。

算法实现

伪代码

1
2
3
4
5
6
7
创建k个点作为K个簇的起始质心（经常随机选择）
当任意一个点的蔟分配结果发生变化时（初始化为True）
	对数据集中的每个数据点，重新分配质心
		对每个质心
			计算质心到数据点之间的距离
		将数据点分配到距其最近的蔟
	对每个蔟，计算蔟中所有点的均值并将均值作为新的质心

实现

因为我们用到的是数值类型数据，这里需要编写一个加载数据集的函数，其返回值是一个矩阵。下面代码应写在一个py文件里，我这里写在kMeans.py文件中。

首先引入相关的头文件：numpy

1
from numpy import *

数据集加载代码

1
2
3
4
5
6
7
8
9
# 加载数据集文件，没有返回类标号的函数
def loadDataSet(fileName):
    dataMat = []
    openfile = open(fileName)    
    for line in openfile.readlines():
        curLine = line.strip().split('\t')
        floatLine = map(float,curLine)
        dataMat.append(floatLine)
    return dataMat

因为在k均值算法中要计算点到质心的距离，所以这里将距离计算写成一个函数，计算欧几里得距离公式：

$$d=\sqrt{(x_1-z_1)^2+…+(x_n-z_n)^2}$$

函数代码如下：

1
2
3
# 计算两个向量的欧氏距离
def distEclud(vecA,vecB):
    return sqrt(sum(power(vecA-vecB,2)))

接下来初始化k个蔟的质心函数centroid

1
2
3
4
5
6
7
8
9
10
# 传入的数据时numpy的矩阵格式
def randCent(dataMat, k):
    n = shape(dataMat)[1]
    centroids = mat(zeros((k,n)))  
    for j in range(n):
        minJ = min(dataMat[:,j]) # 找出矩阵dataMat第j列最小值
        rangeJ = float(max(dataMat[:,j]) - minJ) #计算第j列最大值和最小值的差
        #赋予一个随机质心，它的值在整个数据集的边界之内
        centroids[:,j] = minJ + rangeJ * random.rand(k,1) 
    return centroids #返回一个随机的质心矩阵

K-means算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#返回的第一个变量时质心，第二个是各个簇的分布情况
def kMeans(dataMat,k,distE = distEclud , createCent=randCent):
    m = shape(dataMat)[0]    # 获得行数m
    clusterAssment = mat(zeros((m,2))) # 初试化一个矩阵，用来记录簇索引和存储误差                               
    centroids = createCent(dataMat,k) # 随机的得到一个质心矩阵蔟
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        for i in range(m):    #对每个数据点寻找最近的质心
            minDist = inf; minIndex = -1
            for j in range(k): # 遍历质心蔟，寻找最近的质心    
                distJ1 = distE(centroids[j,:],dataMat[i,:]) #计算数据点和质心的欧式距离
                if distJ1 < minDist: 
                    minDist = distJ1
                    minIndex = j
            if clusterAssment[i,0] != minIndex:
                clusterChanged = True
            clusterAssment[i,:] = minIndex, minDist**2
        print centroids
        for ci in range(k):   #更新质心，将每个族中的点的均值作为质心
            index_all = clusterAssment[:,0].A   #取出样本所属簇的索引值
            value = nonzero(index_all==ci)    #取出所有属于第ci个簇的索引值
            sampleInClust = dataMat[value[0]]     #取出属于第i个簇的所有样本点
            centroids[cent,:] = mean(sampleInClust, axis=0) 
    return centroids, clusterAssment

虽然K-Means算法原理简单，但是也有自身的缺陷：

  • 首先，聚类的簇数K值需要事先给定，但在实际中这个 K 值的选定是非常难以估计的，很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适。
  • Kmeans需要人为地确定初始聚类中心，不同的初始聚类中心可能导致完全不同的聚类结果，不能保证Ｋ-Means算法收敛于全局最优解。
    • 针对此问题，在K-Means的基础上提出了二分K-means算法。该算法首先将所有点看做是一个簇，然后一分为二，找到最小SSE的聚类质心。接着选择其中一个簇继续一分为二，此处哪一个簇需要根据划分后的SSE值来判断。
  • 对离群点敏感。
  • 结果不稳定 （受输入顺序影响）。
  • 时间复杂度高O(nkt)，其中n是对象总数，k是簇数，t是迭代次数。

测试

在控制台调用上述函数，执行下列命令：

1
2
dataMat = mat(loadDataSet('testSet.txt'))
kMeans(dataMat, 4)

运行上面代码后，可以看到print处输出的结果：

[[-3.66087851  2.30869657]
 [ 3.24377288  3.04700412]
 [ 2.52577861 -3.12485493]
 [-2.79672694  3.19201596]]
[[-3.78710372 -1.66790611]
 [ 2.6265299   3.10868015]
 [ 1.62908469 -2.92689085]
 [-2.18799937  3.01824781]]
[[-3.53973889 -2.89384326]
 [ 2.6265299   3.10868015]
 [ 2.65077367 -2.79019029]
 [-2.46154315  2.78737555]]

测试的时候取的k值为4，即簇的个数为4，所以经过3次迭代之后K-均值算法就收敛了。质心会保存在第一个返回值中，第二个是每个点的簇分布情况。k=4是，聚类结果如下：

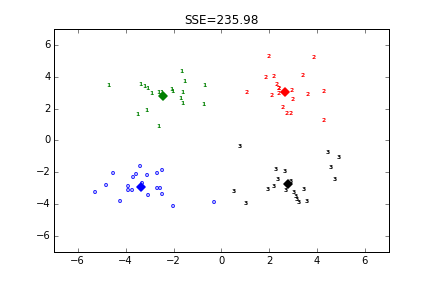
附数据集：https://github.com/csuldw/MachineLearning/blob/master/Kmeans/data/testSet.txt

讨论

1.K-Means算法K值如何选择？

《大数据》中提到：给定一个合适的类簇指标，比如平均半径或直径，只要我们假设的类簇的数目等于或者高于真实的类簇的数目时，该指标上升会很缓慢，而一旦试图得到少于真实数目的类簇时，该指标会急剧上升。

  • 簇的直径是指簇内任意两点之间的最大距离。
  • 簇的半径是指簇内所有点到簇中心距离的最大值。

2. 如何优化K-Means算法搜索的时间复杂度？

可以使用K-D树来缩短最近邻的搜索时间（NN算法都可以使用K-D树来优化时间复杂度）。

3. 如何确定K个簇的初始质心？

1) 选择批次距离尽可能远的K个点

首先随机选择一个点作为第一个初始类簇中心点，然后选择距离该点最远的那个点作为第二个初始类簇中心点，然后再选择距离前两个点的最近距离最大的点作为第三个初始类簇的中心点，以此类推，直至选出K个初始类簇中心点。

2) 选用层次聚类或者Canopy算法进行初始聚类，然后利用这些类簇的中心点作为KMeans算法初始类簇中心点。

聚类扩展：密度聚类、层次聚类。

##　参考文献