在上一篇Deep Learning - CNN原理剖析一文中介绍了卷积神经网络,CNN的层次框架是输入层、卷积层、ReLU层、Pooling层、FC全连接层,其两大主要特性是:局部感知和权值共享。在应用上,CNN主要用于图像分析,然而对于存在上下文关系或是时序特性的场景,如NLP、语音识别等,CCN则表现得很无力。由此便出现了另一种神经网络结构——RNN(Recurrent Neural Networks,循环神经网络)。
RNN介绍
RNN是一类用于处理序列数据的神经网络,它的深度就是时间的长度。那么什么是时序序列数据呢?百度百科:时间序列数据(time series data)是在不同时间上收集到的数据,这类数据是按时间顺序收集到的,用于所描述现象随时间变化的情况。从理论上将,RNN可以保留很长的序列信息,但实践中并非如此,它只能保留短期的信息。下面来看看RNN框架:
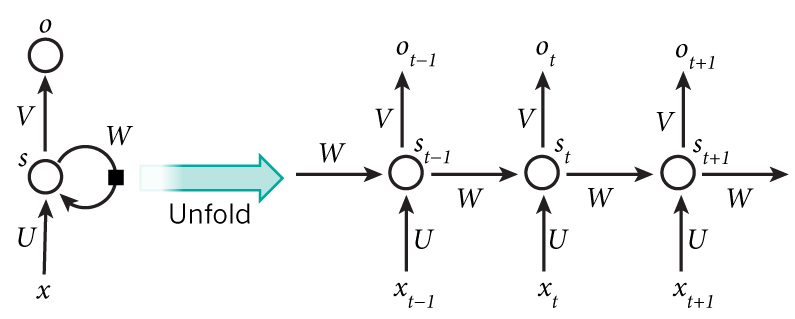
第一眼看到上面的左图,可能会让人觉得迷糊,笔者看到的时候也一样。我们来分析下上面这个图,先看看左边的,一共有六个变量。根据神经网络典型的三层结构,输入层、隐藏层、输出层,我们可以很清楚的确定$x$为输入层,在NLP中,就是一段文本;$o$表示的是输出层,比如情感分类中,就是输出这句话的的情感色彩。中间的$s$属于隐藏状态,$s$会通过输入层和上一个隐藏层不断的叠加。通过展开之后,从图右我们可以看到在不同时刻RNN的计算方式。
- $x_t$是$t$时刻的输入,例如$x_1$表示一段文本中第一个单词的ont-hot 向量。
- $s_t$是$t$时刻的隐藏状态。$s_t$的值是根据上一个隐藏状态与当前时刻的输入进行计算的,即$s_t = f(Ux_t + W s_{t-1})$。激活函数$f$是非线性函数,如tanh或ReLU,$s_{-1}为第一个隐藏层,$通常初始化全为$0$。隐藏状态的内容可以看做是网络的记忆。
- $o_t$是$t$时刻的输出,例如,我们想要预测句子中下一个单词是什么,那么输出便是我们词库的一个概率向量$o_t = softmax(Vs_t)$。由于$o_t$的计算仅仅基于$t$时刻的记忆,而在实际当中,$s_t$通常无法保留过多的记忆,所以隐藏层的循环过程显得有些复杂。
通过上图我们可以看到,RNN每一步都是共享权值(U、V、W)的,基于这一点,与相同层数的DNN相比,RNN需要计算的参数要少很多。
RNN能做什么
RNN对应场景可分为下图集中情况:
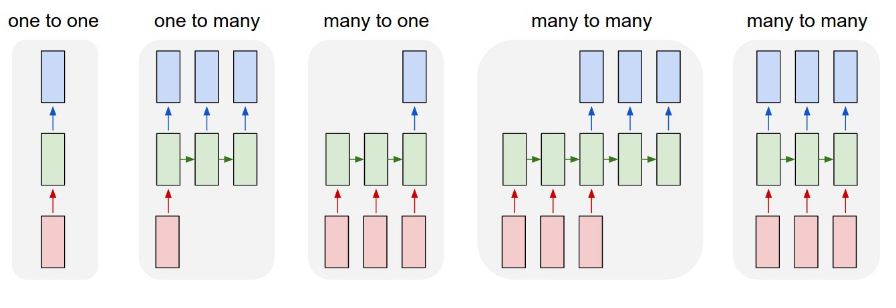
One-to-One
One-to-One每一个输入都有对应的输出,比如词性标注。
Many-to-One
Many-to-One最典型的场景就是文本分类,比如情感识别,输入一段话,最后判断该句话的情感是积极的还是消极的。
One-to-Many
One-to-Many比较典型的场景是图像到文本,输入是一张图片,输出是一段文字,比如图像描述。
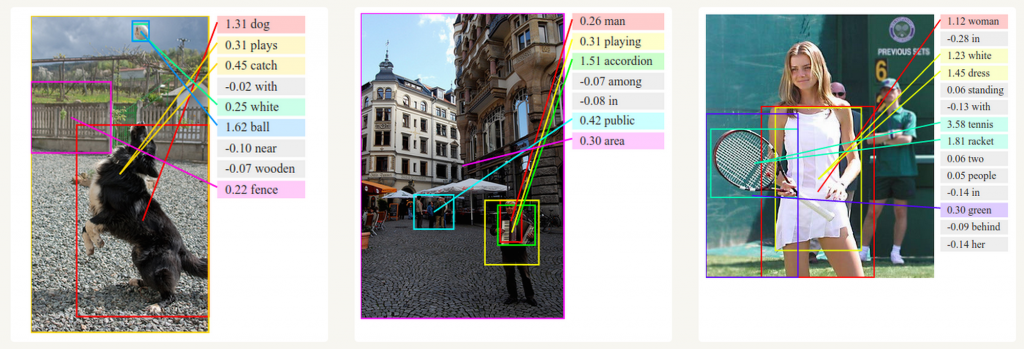
Many-to-Many
机器翻译类似于语言建模,我们输入的是源语言(例如德语)中的一系列单词。我们希望输出目标语言(如英语)中的一系列单词。一个关键的区别是,我们的输出只有在看到整个输入之后才开始输出,因为翻译的每一个单词还得考虑上下文的关系。
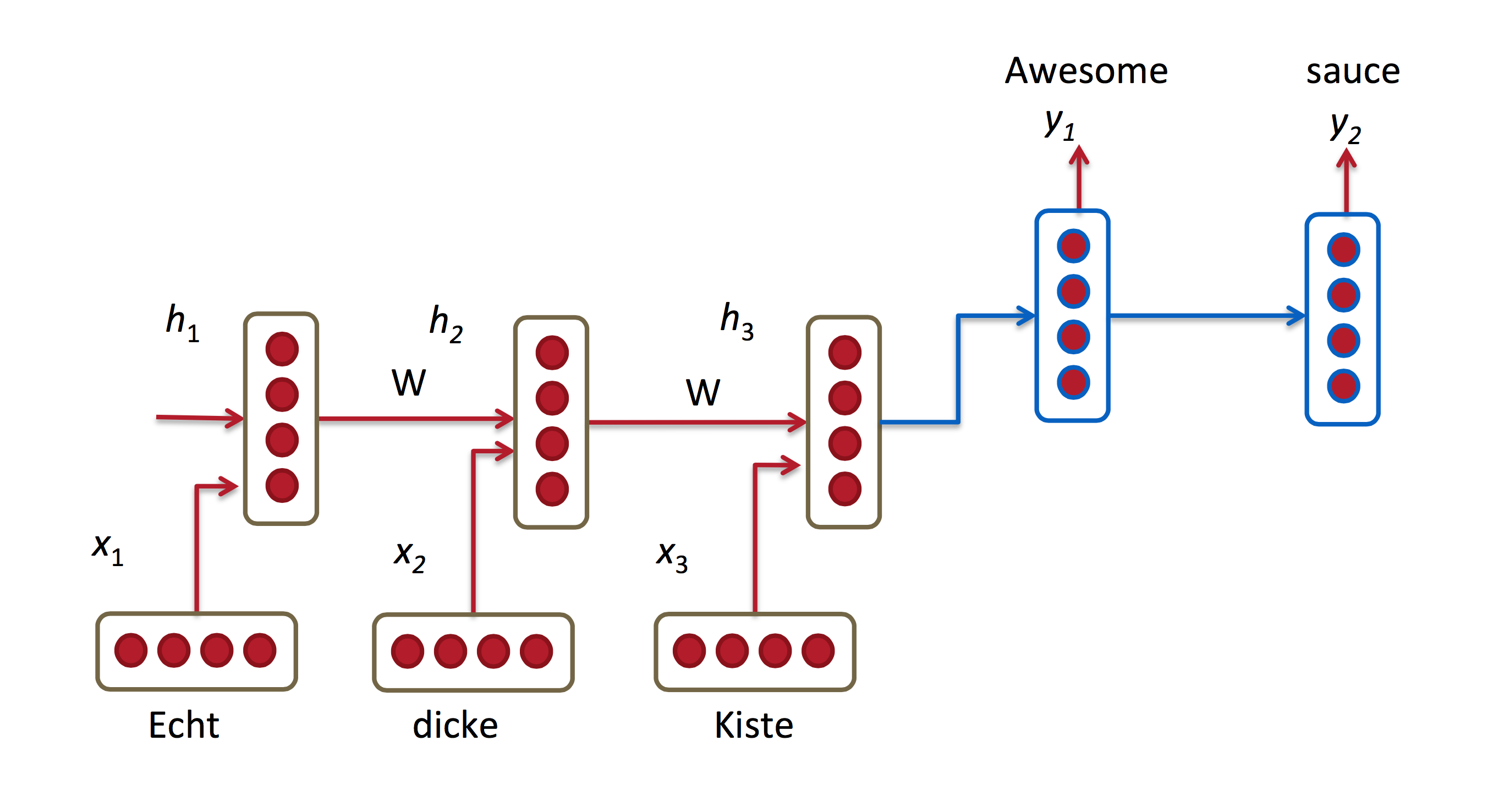
关于机器翻译相关的文章:
- A Recursive Recurrent Neural Network for Statistical Machine Translation
- Sequence to Sequence Learning with Neural Networks
- Joint Language and Translation Modeling with Recurrent Neural Networks
除了机器翻译之外,还有视频帧的分类,都属于M2M。
权值更新推导
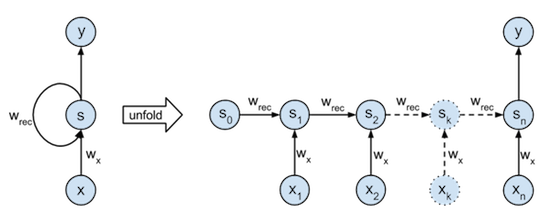
首先我们看看下图,该图是第一张图的细化图,一个完整的RNN结构图。
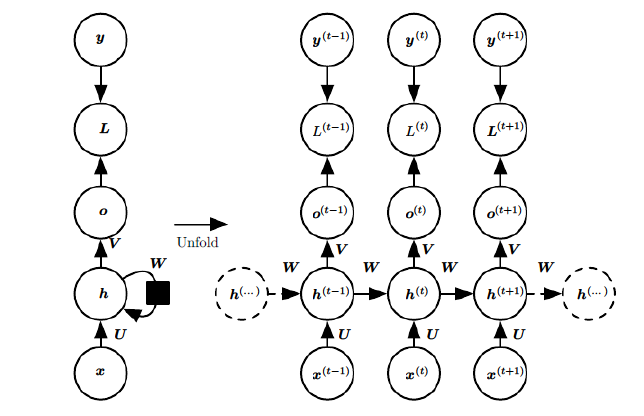
- $x^{(t)}$表示在$t$时刻训练样本的输入。同样的,$x^{(t−1)}$和$x^{(t+1)}$代表在$t−1$和$t+1$时刻训练样本的输入。
- $h(t)$表示$t$时刻模型的隐藏状态。$h^{(t)}$由$t$时刻的输入$x^{(t)}$和$t-1$时刻的隐藏状态$h^{(t−1)}$共同决定。
- $o(t)$表示$t$时刻模型的输出。$o(t)$只由模型当前的隐藏状态$h^{(t)}$)决定。
- $L(t)$表示$t$时刻模型的loss function。
- $y(t)$表示$t$时刻训练样本序列的真实输出。
- $U,W,V$ 这三个矩阵是我们的模型的线性关系参数,它在整个RNN 网络中是共享的,这点和DNN 很不相同。也正因为是共享了,它体现了RNN的模型的“循环反馈”的思想。RNN输入到隐藏的连接由权重矩阵$U$参数化,隐藏到隐藏的循环连接由权重矩阵$w$参数化,隐藏到输出的连接由权重矩阵$V$参数化。
前向传播
根据前向传播的思想,对于任意一个时刻$t$,它的隐藏状态$h^{(t)}$由$x^{(t)}$和$h^{(t−1)}$计算得到,假设$tanh$函数为RNN的隐藏状态的激活函数,那么隐藏状态的计算公式为:
$$
h^{(t)} = tanh(z^{(t)}) = tanh(Ux^{(t)} + Wh^{(t-1)} +b )
\tag{1} \label{1}
$$
$b$为线性关系的偏置项。通过上图,我们可以知道$t$时刻的输出为$o^{(t)}$:
$$
o^{(t)} = Vh^{(t)} +c
\tag{2} \label{2}
$$
假定RNN用于训练分类模型,那么上面最终预测输出这一层的激活函数为softmax,那么最终的预测输出为:
$$
\hat{y}^{(t)} = softmax(o^{(t)})
\tag{3} \label{3}
$$
通过损失函数$L(t)$,比如对数似然损失函数,我们可以量化模型在当前时刻的损失,即$\hat{y}^{(t)}$和$y(t)$的差值。
后向传播
RNN后向传播的思路与DNN是一样的,都是通过梯度下降逐步迭代,关于BP算法,可以参考下之前写的文章Deep Learning - 神经网络与BP算法。基于RNN的模型主要是寻找合适的参数:$U$、$W$、$V$、$b$和$c$。由于RNN存在时序关系,所以RNN的BP算法也叫做BPTT(back-propagation through time)。需要注意的是,RNN共享参数,所以BP算法更新的都是相同的变量$U$、$W$、$V$、$b$和$c$.下面,来看看RNN的权值更新推导,找出损失函数对$U$、$W$、$V$、$b$和$c$的偏导数。
假定我们最终的损失函数为$L$,这里假设为MSE,那么
$$
L = \sum\limits_{t=1}^{\tau}L^{(t)}
\tag{4} \label{4}
$$
输出层的偏导数为:
$$
\frac{\partial L}{\partial o^{(t)}}
= \color{ blue }{\frac{\partial L}{\partial L^{(t)}} } \frac{\partial L^{(t)}} {\partial o^{(t)}}
= \frac{\partial L^{(t)}} {\partial o^{(t)}}
=\hat{y}^{(t)} - y^{(t)}
\tag{5} \label{5}
$$
关于$V$和$c$的梯度计算,公式如下:
$$
\frac{\partial L}{\partial c} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial c} = \sum\limits_{t=1}^{\tau}\frac{\partial L^{(t)}}{\partial o^{(t)}} \frac{\partial o^{(t)}}{\partial c} = \sum\limits_{t=1}^{\tau}\hat{y}^{(t)} - y^{(t)}
\tag{6} \label{6}
$$
$$
\frac{\partial L}{\partial V}
=\sum\limits_{t=1}^{\tau} \frac{\partial L^{(t)}}{\partial V}
= \sum\limits_{t=1}^{\tau} \frac{\partial L^{(t)}}{\partial o^{(t)}} \color{ blue }{\frac{\partial o^{(t)}}{\partial V} }
= \sum\limits_{t=1}^{\tau}(\hat{y}^{(t)} - y^{(t)}) \color{ blue }{(h^{(t)})^T}
\tag{7} \label{7}
$$
对于$W$、$U$、$b$的计算略微复杂,从RNN的模型结构来看,在BP过程时,$t$时刻的梯度损失由当前位置的输出$o^{(t)}$的梯度损失和$t+1$时刻的梯度损失两部分共同决定($t$时刻的输出$o^{(t)}$与$t+1$时刻的隐藏状态$h^{(t+1)}$都调用了$h^{(t)}$)。对于$W$在$t$时刻的梯度损失需要BP迭代计算。我们假定$t$时刻的隐藏状态的梯度为:
$$
\delta^{(t)} = \frac{\partial L}{\partial h^{(t)}}
\tag{8} \label{8}
$$
那么根据$\delta^{(t+1)}$递推$\delta^{(t)}$,我们可以得到下面的结果(由上到下的计算原因是$\eqref{1}$中的激活函数$h$为$tanh$,其导数为$tanh’(x) = 1 - tanh^2(x)$):
$$
\begin{align}
\delta^{(t)}
&=\frac{\partial L}{\partial o^{(t)}} \color{ blue }{\frac{\partial o^{(t)}}{\partial h^{(t)}}} + \color{ red }{\frac{\partial L}{\partial h^{(t+1)}}}\frac{\partial h^{(t+1)}}{\partial h^{(t)}} \\
&= \color{ blue }{V^T}(\hat{y}^{(t)} - y^{(t)}) + W^T \color{ red }{\delta^{(t+1)}}diag(1-(h^{(t+1)})^2)
\end{align}
\tag{9} \label{9}
$$
其中$diag(1-(h^{(t+1)})^2)$表示$1-(h^{(t+1)})^2$的对角矩阵,是关于t+1时刻与隐藏单元的双正切的Jacobian。假设最后一个时间步为$\tau$时刻,那么:
$$
\delta^{(\tau)} =\frac{\partial L}{\partial o^{(\tau)}} \frac{\partial o^{(\tau)}}{\partial h^{(\tau)}} = V^T(\hat{y}^{(\tau)} - y^{(\tau)})
\tag{10} \label{10}
$$
有了$\delta^{(t)}$,计算$W、U、b$的梯度就容易了,基于公式$\eqref{1}$,可以得到$L$对各个隐藏层各个参数的偏导如下:
$$
\frac{\partial L}{\partial W}
= \sum\limits_{t=1}^{\tau} \color{ blue }{\frac{\partial L}{\partial h^{(t)}}} \frac{\partial h^{(t)}}{\partial W} = \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2) \color{ blue }{\delta^{(t)}}(h^{(t-1)})^T
\tag{11} \label{11}
$$
$$
\frac{\partial L}{\partial U}
= \sum\limits_{t=1}^{\tau} \color{ blue }{\frac{\partial L}{\partial h^{(t)}}} \frac{\partial h^{(t)}}{\partial U}
= \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2) \color{ blue }{\delta^{(t)}}(x^{(t)})^T
\tag{12} \label{12}
$$
$$
\frac{\partial L}{\partial b}
= \sum\limits_{t=1}^{\tau}\color{ blue }{\frac{\partial L}{\partial h^{(t)}}} \frac{\partial h^{(t)}}{\partial b}
= \sum\limits_{t=1}^{\tau}diag(1-(h^{(t)})^2) \color{ blue }{\delta^{(t)}}
\tag{13} \label{13}
$$
得到损失函数与偏导数的关系之后,我们就可以采用基于梯度的优化方法如SGD进行参数训练,逐步逼近最优解。
梯度爆炸与梯度消失
在CNN中,当我们的网络层次比较深的时候,如果激活函数为sigmoid或tanh函数,则会出现“梯度消失”的现象。对于tanh和sigmoid函数,它们在两端的梯度值都为0。在CNN中,当前时刻的梯度为0会使得前面层的梯度也为0。同时,矩阵出现比较小的值的时候,当多个矩阵相乘就会使梯度值以指数级速度下降,最终在几步后完全消失。比较远的时刻的梯度值最终会等于0,这些时刻的状态对学习过程没有帮助,导致你无法学习到长距离依赖。那么在RNN中,又会出现什么现象呢?
根据RNN上面BPTT推导,我们可以得到$\eqref{11}$、$\eqref{12}$、$\eqref{13}$三个表达式,这三个表达式都存在一个$\delta^{(t)}$,表示$t$时刻隐藏状态的梯度,根据$\eqref{9}$我们可以看到$\delta^{(t)}$是通过迭代计算得到,与$\delta^{(t+1)}$强相关,我们把$\eqref{9}$式变化一下:
$$
\begin{align}
\delta^{(t)}
&=\frac{\partial L}{\partial o^{(t)}} \color{ blue }{\frac{\partial o^{(t)}}{\partial h^{(t)}}} + \frac{\partial L}{\partial h^{(t+1)}}\frac{\partial h^{(t+1)}}{\partial h^{(t)}} \\
&= \color{ blue }{V^T}(\hat{y}^{(t)} - y^{(t)}) + \color{ red }{W^T \delta^{(t+1)} * tanh’}
\end{align}
\tag{14} \label{14}
$$
仔细观察上面的式子,当$W$初始化值很大时,由于每个$\delta$都存在$W$,而$\delta^{(t)}$等于$W$与$\delta^{(t+1)}$的乘机,因此多个$W$相乘,最终导致“梯度爆炸”现象;另外,由于$\delta^{(t)}$与$\delta^{(t+1)}$之间还有一个$tanh’$ ($tanh’\leq 1$),当层次比较深的时候,就会出现很多个$tanh’$相乘,最终会使得梯度越来越小,逐渐趋近0,随后“梯度消失”现象也就出现了。
通常梯度消失比梯度爆炸受到了更多的关注,其原因有二:
- “梯度爆炸”出现之后容易发现,梯度值会变成NaN,从而导致程序崩溃,容易确定问题并fixed;
- “梯度消失”的出现不会那么明显,处理起来不方便。
当然,神经网络经过多年的发展,已经有一些方法解决了“梯度消失”问题的办法。比如
- 合适的初始化矩阵$W$可以适当的减小梯度消失效应;
- 在损失函数上加上正则也能起一定作用;
- 选择择ReLU而不是sigmoid和tanh作为激活函数。ReLU的导数是常数值0或1,所以不可能会引起梯度消失。
这些方法并不是最好的,还有更好的解决方法,也就是采用LSTM或GRU,本文暂且不做介绍。
Conclusion
上面总结了通用的RNN模型和前向与反向传播过程。RNN虽然理论上可以很漂亮的解决序列数据的训练,但是它也像DNN一样存在“梯度消失”的问题,当序列很长的时候问题尤其严重。因此,上面的RNN模型一般不能直接用于应用领域。在语音识别,手写书别以及机器翻译等NLP领域实际应用比较广泛的是基于RNN模型的一个变体LSTM,关于LSTM的细节,将在下一节进行介绍。一大串的公式,敲得头头昏脑涨,喝杯咖啡,休息休息!
说明:文章公式较多,如有攥写错误,还请读者指出,深表感谢!