FM算法原理分析与实践

“学而时习之，不亦说乎”，趁着过年几天假期，多写几篇文章。上一篇文章基于Embedding的推荐系统召回策略介绍的是一种召回方法，本文将介绍一种用于推荐系统排序阶段的方法FM，全称Factorization Machines，该算法的目的是解决稀疏数据下的特征组合问题，被广泛应用于广告推荐等CTR预估场景。关于FM算法的介绍数不胜数，读者也可以去阅读paper。本文纯粹是笔者实践过程中的个人总结，内容简要浅显，不敢与其他行家媲美，如若读者在阅读过程中发现疑问，还请留言告知，谢谢！

简介

FM是Steffen Rendle在2010年提出的，FM算法的核心在于特征组合，以此来减少人工参与特征组合工作。对于FM，其优势可分以下三点:

FM能处理数据高度稀疏场景，SVM则不能；
FM具有线性的计算复杂度，而SVM依赖于support vector。
FM能够在任意的实数特征向量中生效。

FM原理

FM的数据结构如下：

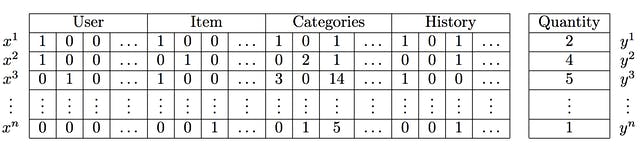
FM特征数据结构：User相关、Item相关、类别相关的特征、历史行为数据特征等等，最后一列可看作是User对Item评分

FM通过不同特征的组合，生成新的含义。然而，特征组合也随之带来一些问题：

特征之间两两组合容易导致维度灾难；
组合后的特征未必有效，可能存在特征冗余现象；
组合后特征样本非常稀疏，如果原始样本中不存在对应的组合，则无法学习参数，那么该组合就显得无效。

虽然有这些缺点，但是也并不影响FM在广告推荐领域的地位，每个算法都有风靡一时的过去，抱着敬畏之心的态度去学习是没问题的。下面，来看看FM的算法原理。

目标函数

我们知道，线性模型的目标函数为：

$$
y = w_{0} + \sum_{i=1}^{n} w_{i} x_{i}
\tag{1} \label{1}
$$

其中$n$表示样本的特征数量，$w_{0}$为偏置，$x_{i}$表示第$i$个特征的值，后面一项为特征的Linear combination。FM增加了特征交叉组合部分，表达式如下：

$$
y = w_{0} + \sum_{i=1}^{n} w_{i} x_{i} + \color{blue} {\sum_{i=1}^{n-1} \sum_{j=i+1}^{n} w_{ij} x_{i} x_{j}}
\tag{2} \label{2}
$$

其中$w_{0}$、$w_{i}$、$w_{ij}$是模型参数。从公式来看，模型前半部分就是普通的LR线性组合[No Problem]，后半部分的交叉项：特征组合。首先，单从模型表达能力上来看，FM是要强于LR的，至少它不会比LR弱，当交叉项参数$w_{ij}$全为0的时候，整个模型就退化为普通的LR模型。对于有$n$个特征的模型，特征组合的参数数量共有$1+2+3+\cdots + n-1=\frac{n(n-1)}{2}$个，并且任意两个参数之间是独立的。所以说特征数量比较多的时候，特征组合之后，维度自然而然就高了。

代数知识：

任意一个实对称矩阵（正定矩阵）$W$都存在一个矩阵$V$，使得 $W=V.V^{T}$成立。

类似地，所有二次项参数$\omega_{ij}$可以组成一个对称阵$W$（为了方便说明FM的由来，对角元素可以设置为正实数），那么这个矩阵就可以分解为$W=V^TV$，$V$ 的第$j$列($v_{j}$)便是第$j$维特征($x_{j}$)的隐向量。

$$
\hat{y}(X) = \omega_{0}+\sum_{i=1}^{n}{\omega_{i}x_{i}}+\sum_{i=1}^{n-1}{\sum_{j=i+1}^{n} \color{red}{<v_{i},v_{j}>x_{i}x_{j}}}
\tag{3} \label{3}
$$

需要估计的参数有$\omega_{0}∈ R$，$\omega_{i}∈ R$，$V∈ R$，$< \cdot, \cdot>$是长度为$k$的两个向量的点乘，公式如下：

$$<v_{i},v_{j}> = \sum_{f=1}^{k}{v_{i,f}\cdot v_{j,f}}
\tag{4} \label{4}
$$

上面的公式$\eqref{3}$，$\eqref{4}$中，

$\omega_{0}$为全局偏置；
$\omega_{i}$是模型第$i$个变量的权重;
$\omega_{ij} = < v_{i}, v_{j}>$特征$i$和$j$的交叉权重;
$v_{i} $是第$i$维特征的隐向量;
$<\cdot, \cdot>$代表向量点积;
$k(k<<n)$为隐向量的长度，包含 $k$ 个描述特征的因子。

根据公式$\eqref{2}$，二次项的参数数量减少为 $kn $个，远少于多项式模型的参数数量。另外，参数因子化使得 $x_{h}x_{i}$ 的参数和 $x_{i}x_{j}$ 的参数不再是相互独立的，因此我们可以在样本稀疏的情况下相对合理地估计FM的二次项参数。具体来说，$x_{h}x_{i}$ 和 $x_{i}x_{j}$的系数分别为 $<v_{h},v_{i}>$ 和 $<v_{i},v_{j}>$ ，它们之间有共同项 $v_{i}$ 。也就是说，所有包含“ $x_{i}$ 的非零组合特征”（存在某个 $j \ne i$ ，使得 $x_{i}x_{j}\neq 0$ ）的样本都可以用来学习隐向量$v_{i}$，这很大程度上避免了数据稀疏性造成的影响。而在多项式模型中,$w_{hi}$ 和 $w_{ij}$ 是相互独立的。

显而易见，公式$\eqref{3}$是一个通用的拟合方程，可以采用不同的损失函数用于解决regression、classification等问题，比如可以采用MSE（Mean Square Error）loss function来求解回归问题，也可以采用Hinge/Cross-Entropy loss来求解分类问题。当然，在进行二元分类时，FM的输出需要使用sigmoid函数进行变换，该原理与LR是一样的。直观上看，FM的复杂度是 $O(kn^2)$ 。但是，通过公式$\eqref{4}$的等式，FM的二次项可以化简，其复杂度可以优化到 $O(kn)$ 。由此可见，FM可以在线性时间对新样本作出预测。

公式$\eqref{3}$的推导

$$
ab+ac+bc = \frac{1}{2}\left[(a+b+c)^2-(a^2+b^2+c^2) \right]
\tag{5} \label{5}
$$

$$
\begin{align} \sum_{i=1}^{n-1}{\sum_{j=i+1}^{n}{<v_i,v_j>x_ix_j}}
&= \frac{1}{2}\sum_{i=1}^{n}{\sum_{j=1}^{n}{<v_i,v_j>x_ix_j}} - \frac{1}{2} {\sum_{i=1}^{n}{<v_i,v_i>x_ix_i}} \\
&= \frac{1}{2} \left( \sum_{i=1}^{n}{\sum_{j=1}^{n}{\sum_{f=1}^{k}{v_{i,f}v_{j,f}x_ix_j}}} - \sum_{i=1}^{n}{\sum_{f=1}^{k}{v_{i,f}v_{i,f}x_ix_i}} \right) \\
&= \frac{1}{2}\sum_{f=1}^{k}{\left[ \left( \sum_{i=1}^{n}{v_{i,f}x_i} \right) \cdot \left( \sum_{j=1}^{n}{v_{j,f}x_j} \right) - \sum_{i=1}^{n}{v_{i,f}^2 x_i^2} \right]} \\
&= \frac{1}{2}\sum_{f=1}^{k}{\left[ \left( \sum_{i=1}^{n}{v_{i,f}x_i} \right)^2 - \sum_{i=1}^{n}{v_{i,f}^2 x_i^2} \right]} \end{align}
\tag{6} \label{6}
$$

解释：

$v_{i,f}$ 是一个具体的值；
第1个等号：对称矩阵 $W$ 对角线上半部分；
第2个等号：把向量内积 $v_{i}$,$v_{j}$ 展开成累加和的形式；
第3个等号：提出公共部分；
第4个等号： $i$ 和 $j$ 相当于是一样的，表示成平方过程。

SGD训练参数

使用SGD进行训练，可以推导出SGD的参数更新方式：

$$
\begin{equation}
\frac{\partial \hat{y}(x)}{\partial \theta} = \left\{\begin{array}
{lr} 1, & if \ \theta\ is\ \omega_{0} \\
x_{i}, & if\ \theta\ is\ \omega_i \\
x_{i} \sum_{j=1}^{n}{v_{j,f} \ x_{j} - v_{i,f} \ x_{i}^2} & if\ \theta\ is\ v_{i,f} \end{array} \right.
\end{equation}
\tag{7} \label{7}
$$

上式中，$\sum_{j=1}^{n} v_{j,f} \ x_{j}$ 的计算与变量$i$相互独立，因此可以预先计算得到。每个梯度的计算时间复杂度都为$O(1)$，模型的参数总数量为 $nk + n + 1$，在数据稀疏条件下，参数更新所需要的所有时间为$ O(k n)$。

实验

Windows下安装pyfm

pyfm install：将pyFM 下载到本地，解压后去掉setup.py文件里面的libraries=[“m”]一行,然后采用python setup.py install安装即可.

分类模型

FM可以用来进行分类，为了方便，这里使用sklearn里面的iris数据集作为实验数据，将target等于2的作为正样本，其余作为负样本，并采用train_test_split方法划分训练集与测试集，然后通过FM构建分类模型，并通过测试集验证FM的效果。完整Demo代码如下（Github地址：pyfm_demo.py）：

# -*- coding: utf-8 -*-
"""
Created on Sun Jan 27 23:49:24 2019
@author: liudiwei
"""
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from pyfm import pylibfm
from sklearn.feature_extraction import DictVectorizer

def load_data():
    """
    调用sklearn的iris数据集，筛选正负样本并构造切分训练测试数据集
    """
    iris_data = load_iris()
    X = iris_data['data']
    y = iris_data['target'] == 2
    data = [ {v: k for k, v in dict(zip(i, range(len(i)))).items()}  for i in X]
    X_train,X_test,y_train, y_test = train_test_split(data,y, test_size=0.3, random_state=0)
    return X_train,X_test,y_train, y_test

X_train,X_test,y_train, y_test = load_data()

v = DictVectorizer()
X_train = v.fit_transform(X_train)
X_test = v.transform(X_test)

fm = pylibfm.FM(num_factors=2, 
                num_iter=200, 
                verbose=True, 
                task="classification", 
                initial_learning_rate=0.001, 
                learning_rate_schedule="optimal")

fm.fit(X_train, y_train)

y_preds = fm.predict(X_test)
y_preds_label = y_preds > 0.5
from sklearn.metrics import log_loss,accuracy_score
print ("Validation log loss: %.4f" % log_loss(y_test, y_preds))
print ("accuracy: %.4f" % accuracy_score(y_test, y_preds_label))

对于上面的FM模型，摘录了pyFM的一部分参数，其它参数可参考官方解释。

num_factors : int, The dimensionality of the factorized 2-way interactions
num_iter : int, 迭代次数
learning_rate_schedule（可选参数） : string类型, 学习率迭代参数值:
- constant: $\eta = \eta_0$
- optimal: $\eta = \frac{1}{t+t_0}$ [default]
- invscaling: $\eta = \eta_0 / pow(t, power\_t)$
initial_learning_rate : double, 初始时的学习率，默认等于 0.01
task : 模型任务类型，string
- regression: Labels 为实数值.
- classification: Labels 为1或0.
verbose : bool，是否需要打印当前迭代时的训练误差（training error）.
power_t : double, The exponent for inverse scaling learning rate [默认值 0.5].
t0 : double，learning_rate_schedule的初始值. 默认值 0.001.

实验结果

通过上面代码，跑出的结果如下（注：每次实验结果不一定相同）：

1
2
3

Training log loss: 0.12161
Validation log loss: 0.1868
accuracy: 0.9778

结束语

OK，关于FM的介绍暂且结束，FM的计算是比较耗内存的，特征维度超过100，两两组合之后，特征维度就达到1w+，维度增加带来的就是计算量的剧增，跑实验的话，还是需要硬件支撑的。所以也因此衍生出FFM算法（Field-aware FM），主要是对特征进行分组然后进行组合。关于FFM的细节，后续在补充吧！

简介