继前两篇文章Boosting模型:GBDT原理介绍和CTR预估经典模型:GBDT+LR之后,本文将继续探究下一个Boosting模型:XGBoost,全称eXtreme Gradient Boosting。XGBoost,听着名子就觉得特霸气,给人一种威风四面、震慑八方的实觉。事实上,其在实际比赛和项目实践中的效果也绝不含糊,名副其实呀!具体的数据这里就不展开了,明白就行。XGBoost本身是GBDT的一个高性能的开源库,是陈天奇等人于2014年开发,即可用于分类,也可用于回归。本文主要是介绍XGBoost的原理,同时深入分析下其在GBDT的基础上做了哪些改进点。关于XGBoost的实践,可以参考A Beginner’s guide to XGBoost,是一篇很好的入门级应用教程。
阅读本文之前如果对决策树相关算法不太了解,可以参考笔者以前写的文章(仅供参考):
前言
XGBoost的原始paper将XGBoost的各个点都介绍的非常详细,有耐心的可以细细品味一下:XGBoost: A Scalable Tree Boosting System。本文可以说是一篇paper读后小结,顺便为了内容实用点,顺便附上自己的小demo,便于后续回顾,如有杠精者,还请绕道而行哈。OK,下面进入正文吧!
原理剖析
本章节将从以下几个方面介绍XGBoost:
- Tree Ensemble Model: 提升树模型
- Object Function:XGBoost 目标函数及其求解
- Optimization:寻找最佳分裂点
Tree Ensemble Model
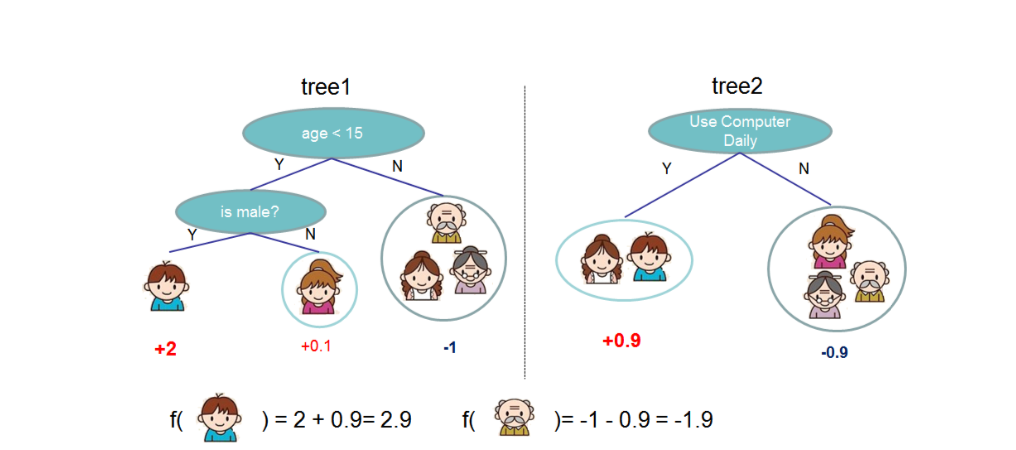
首先,XGBoost与GBDT一样,也是boosting模型,对于boosting decision tree, 下面这张图片可以很好的表达出来(引自XGBoost paper):
给定$n$个样本,$m$个特征的数据集$D= \left \{ (X_i, y_i) \right \} (|D|=n, X_i \in \mathbb{R}^m, y_i \in \mathbb{R})$,提升树模型采用K次迭代的结果作为输出结果。对于$X_i$的输出为$\hat{y}_i$,表达式为:
$$
\hat{y}_i = \phi(X_i) = \sum_{k=1}^K f_{k}(X_i), \ \ \ f_k \in F
\tag{1}\label{1}
$$
其中$F= \left \{ f(X)=w_{q(X)} \right \} (q:\mathbb{R} ^m \rightarrow T, w \in \mathbb{R}^T)$,表示提升树结构空间集,各个变量的含义如下:
- $q$表示树的结构,可以将样本映射到相应的叶子节点;
- $T$表示提升树叶子节点的数量;
- 每个$f_k$都对应独立的树结构$q$和权重$w$,
Object Function
XGBoost的目标函数表达式与GBDT不一样,有着进一步的优化,如下:
$$
L(\phi) = \underbrace{\sum_{i} l(\hat{y}_i, y_i)}_{损失函数项} + \underbrace{\sum_k \Omega(f_k)}_{正则项}
\tag{2}\label{2}
$$
上式看起来很简单,分两部分,第一部分为loss function,第二部分为regularization。各个变量的含义:$y_i$为true label,$\hat{y}_i$为predicted label,$l$为损失函数,$f_k$则表示第k颗树的结构,$\Omega$为正则项,表达式如下:
$$
\Omega(f) = \gamma T + \frac{1}{2} \lambda \parallel w \parallel ^2
\tag{3}\label{3}
$$
在XBGoost里面,正则项又包含两部分:一部分是提升树叶子节点的数量$T$,用于控制树的复杂度,可以达到剪枝的效果;另一部分为每颗树的叶子节点的权重$w$的平方和。正则项可以让学习器尽可能的避免over-fitting。 通过上面的目标函数,XGBoost的每颗子树就会倾向于学习比较简单的树,另外,当正则项参数为0时,目标表达式就会退化为传统的gradient tree boosting模型。
目标函数求解
对于上面的目标函数,如何求取最优解呢?对于损失函数部分,XGBoost采用了二阶泰勒展开式。可能有的童鞋会问,二阶泰勒展开式是什么样的,大学学的都忘记差不多了。没关系,快速传送门进Wiki,仔细回顾下:Taylor’s theorem.
对于XGBoost模型,对于第$t$次迭代,其表达式可扩展为:
$$
L^{(t)} = \sum_{i}^{n} l(y_{i}, \hat{y_{i}}^{(t-1)}+f_{t}(X_{i})) + \Omega(f_k)
\tag{4}\label{4}
$$
我们对上面的式子通过泰勒展开式展开,可以得到如下表达式:
$$
L^{(t)} \simeq \sum_{i}^{n} \left [ \color{red}{l(y_{i}, \hat{y_i}^{(t-1)}) + g_i \ f_t(X_i) + h_i \ f_t^2(X_i))} \right ] + \Omega(f_t)
\tag{5}\label{5}
$$
红色部分为泰勒展开式部分,其中$g_i = \partial _{ \hat{y}^{(t-1)}} \ l(y_{i}, \ \hat{y}^{(t-1)})$, $h_i = \partial^2 _{ \hat{y}^{(t-1)}} \ \ l(y_{i}, \ \hat{y}^{(t-1)})$,分别为损失函数的一阶和二阶梯度。在计算过程中,我们还可以忽略常数项$l(y_i, \hat{y_i}^{(t-1)})$(表示的是目标值与$t-1$次迭代输出的预测值的差,第$t$并不会优化这一项,同时值也是固定的),因此,目标式子可以简化为:
$$
\hat{L}^{(t)}
= \sum_{i}^{n} \left [ g_i \ f_t(X_i) + h_i \ f_t^2(X_i)) \right ] + \Omega(f_t)
\tag{6}\label{6}
$$
根据上式可以看出,目标函数会同时依赖每个数据点的在损失函数上的一阶导数和二阶导数。此外,我们看到右侧还有个正则部分,可以将正则项公式\eqref{3}代入进去,扩展公式可以进一步化解:
$$
\begin{aligned}
\hat{L}^{(t)}
&= \underbrace{\sum_{i}^{n} \left [ g_i \ f_t(X_i) + h_i \ f_t^2(X_i)) \right ]}_{对样本进行积累} + \color{red}{ \gamma T + \frac{1}{2} \lambda \underbrace{\sum_{j=1}^{T} \parallel w_j \parallel ^2}_{对叶子节点进行积累}} \\
&= \sum_{i}^{n} \left [ g_i \ \color{blue}{w_{q(X_i)}} + h_i \color{blue}{\ w_{q(X_i)}^2} \right ] + \gamma T + \frac{1}{2} \lambda \sum_{j=1}^{T} \parallel w_j \parallel ^2 \\
&= \sum_{j=1}^{T}\left[ (\sum_{i \in I_j} g_i) w_j + \frac{1}{2} (\sum_{i\in I_{j}} h_i + \lambda ) w_j^2 \right] + \gamma T
\end{aligned}
\tag{7}\label{7}
$$
公式\eqref{7}第一行中的$f_t(X_i) 等于w_{q(X_i)}$,表示第$t$次迭代中(下标表示迭代次数),样本$X_i$落在第$t$个树结构$f_t$中某个叶子节点的叶子权重值,代入后得到第二行,从第二行到第三行只是将各个样本的权重与一阶导和二阶导乘积之和,按照叶子节点进行分组,分组归并到各个叶子节点上的样本之和。最后化解得到第三行表达式,其为参数$w$的函数,为了求解它,我们可以通过求导并令导数等于0来求出$w$的极值点,然后将其回代到公式中,计算出目标表达式的值:
$$
\frac{\partial \hat{L}^{(t)}}{\partial w_j} = \sum_{i \in I_j} g_i + (\sum_{i\in I_{j}} h_i + \lambda ) w_j =0
\tag{8}\label{8}
$$
可以计算得到:
$$
w_j^{*} = -\frac{\sum_{i \in I_j} g_i}{\sum_{i\in I_{j}} h_i + \lambda }
\tag{9}\label{9}
$$
将公式\eqref{9}代入到公式\eqref{7},可以推导出目标函数的表达式:
$$
\begin{aligned}
\hat{L}^{(t)}
&= \sum_{j=1}^{T}\left[ (\sum_{i \in I_j} g_i) \color{blue}{(-\frac{\sum_{i \in I_j} g_i}{\sum_{i\in I_{j}} h_i + \lambda })} + \frac{1}{2} (\sum_{i\in I_{j}} h_i + \lambda ) \color{blue}{(-\frac{\sum_{i \in I_j} g_i}{\sum_{i\in I_{j}} h_i + \lambda })^2} \right] + \gamma T \\
&= \sum_{j=1}^{T}\left[ (-\frac{(\sum_{i \in I_j} g_i)^2}{\sum_{i\in I_{j}} h_i + \lambda }) + \frac{1}{2} (\frac{(\sum_{i \in I_j} g_i)^2}{\sum_{i\in I_{j}} h_i + \lambda }) \right] + \gamma T \\
&= -\frac{1}{2} \sum_{j=1}^{T} \frac{(\sum_{i \in I_j} g_i)^2}{\sum_{i\in I_{j}} h_i + \lambda } + \gamma T \\
\end{aligned}
\tag{10}\label{10}
$$
公式\eqref{10}表示的就是第$t$次迭代数的结构score,表示各个叶子节点上各个样本的一阶平方和与二阶加和之商的加和再加上树结构复杂度控制项$\gamma T$。应用公式\eqref{10},只需要计算出每个叶子节点上各个样本的一阶梯度和二阶梯度的统计信息,就可以计算出整颗树的结构score,下图是XGBoost paper里面的图解:

对公式\eqref{10}进行简化,就可以得到上图的结果:
$$
obj=- \frac{1}{2}\sum_{j=1}^T \left[{\color{red}{\frac{G_j^2}{H_j+\lambda}} } \right] +\gamma T
$$
那么对于决策树的单个节点,该如何进行划分呢?XGBoost与之前的GBDT、RF、ID3等树模型的计算方法都不一样,但是有一个共性就是计算分裂增益,通过比较分裂增益选择特征的切分点。分裂增益大小计算如下(对于单颗树而言,公式\eqref{10}中的$T=1$),分裂增益值为$L - L_{left} - L_{right} $,推导步骤如下:
$$
\begin{aligned}
L_split
&= L - L_{left} - L_{right} \\
&= \left [ -\frac{1}{2} \frac{(\sum_{i \in I } g_i)^2}{\sum_{i \in I} h_i + \lambda } + \gamma \right] - \left[ -\frac{1}{2} \frac{(\sum_{i \in I_{L} } g_i)^2}{\sum_{i \in I_{L}} h_i + \lambda } + \gamma \right ] - \left [\frac{1}{2} \frac{(\sum_{i \in I_{R} } g_i)^2}{\sum_{i \in I_{R}} h_i + \lambda } + \gamma\right] \\
&= \color{red}{\frac{1}{2}\left [ \frac{(\sum_{i \in I_{L} } g_i)^2}{\sum_{i \in I_{L}} h_i + \lambda } + \frac{(\sum_{i \in I_{R} } g_i)^2}{\sum_{i \in I_{R}} h_i + \lambda } - \frac{(\sum_{i \in I } g_i)^2}{\sum_{i \in I} h_i + \lambda } \right] - \gamma}
\end{aligned}
\tag{11}\label{11}
$$
通过上式就可以计算出分裂的增益,然后确定分裂方式。关键是如何计算出最优分裂点呢?
寻找最佳分裂点
第一种是Exact Greedy Algorithm,一种贪心算法,列举出每个特征每个切分点的增益,然后将增益最大的切分点作为分裂点,这种方法固然会寻找到最优点,但是计算量特别大:

第二种是Approximate Algorithm,近似算法,首先根据特征的百分位数获取候选的划分点(采用的是Weighted Quantile Sketch),然后将连续特征映射到采用候选值划分之后的若干个bucket中,然后基于划分数据数据的切分点采用上面的方式计算出最大的增益点,可在一定程度上提升算法的性能。

在XGBoost paper提到,采用的是样本的二阶梯度$h_i$作为样本的权重,关于Weighted Quantile Sketch为什么采用$h_i$作为权重,可以通过化解目标表达式子\eqref{6}得到(原paper符号有误,请注意):
$$
\begin{aligned}
\sum_{i=1}^n[g_if_t(x_i) + \frac{1}{2}h_if_t^2(x_i) ]
&= \sum_{i=1}^n\frac{1}{2}h_i[f_t^2(x_i) - 2f_t(x_i)(-\frac{g_i}{h_i}) + \underbrace{\color{blue}{(\frac{g_i}{h_i})^2 - (\frac{g_i}{h_i})^2}}_{构建平方项}] \\
&=\sum_{i=1}^n\frac{1}{2}h_i[f_t(x_i) - (-\frac{g_i}{h_i})]^2 + \color{blue}{constant} \\
\end{aligned}
$$
关于Weighted Quantile Sketch算法,的确有点复杂,有兴趣的可以参考这篇博文笔记:XGBoost解读(2)–近似分割算法。
第三种是针对稀疏特征的分裂方式,XGBoost可以自动学习稀疏特征的分裂方向:

Sparsity Aware Split Finding算法会对比将特征值为missing的样本分配到左叶子结点和右叶子结点的两种情形,还可以为缺失值或者指定的值指定默认分裂方向,这中方式可以大大提升算法的效率,原paper中给出了具体的量化:50倍。 这种方式对性能的提升确实是非常可观的。
XGBoost特点
上面介绍了XGBoost的原理,那么具体跟GBDT有哪些异同点呢?这里来归纳下XGBoost的模型特性:
- 目标表达式:XGBoost优化了GBDT的目标函数。一方面,在GBDT的基础上加入了正则项,包括叶子节点的个数和每个叶子节点输出的L2模的平方和,正则项可以控制树的复杂度,让模型倾向于学习简单的模型,防止过拟合;另外,XGBoost还支持线性分类器,传统的GBDT是以CART算法作为基学习器。
- Shrinkage:对每棵树的预测结果采用了shrinkage,相当于学习率,降低模型对单颗树的依赖,提升模型的泛化能力。
- 列采样:XGBoost借助了RF的优点,采用了列采样,进一步防止过拟合,加速训练过程,而传统的GBDT则没有列采样。
- 优化方法:XGBoost对损失函数的展开采用了一阶梯度和二阶梯度,而传统的GBDT只采用了一阶梯度。
- 增益计算:对分裂依据进行了优化。不同于CART算法,XGBoost采用了新的基于一阶导数和二阶导数的统计信息作为树的结构score,采用分列前的结构与分裂后的结构score的增益作为分裂依据,选择增益最大的特征值作为分裂点,替代了回归树的误差平方和。
- 最佳增益节点查找:XGBoost在寻找最佳分离点的方式上采用了近似算法,基于权重的分位数划分方式(权重为二阶梯度$h_i$):Weighted Quantile Sketch。主要是对特征取值进行分桶,然后基于桶的值计算增益。
- 预排序。在寻找最佳增益节点时,将所有数据放入内存进行计算,得到预排序结果,然后在计算分裂增益的时候直接调用。
- 稀疏值处理:XGBoost可以自动学习稀疏值的分裂方向,也可以指定默认方向,这种方式大大可以大大提升模型的性能。
- 并行方式:XGBoost的并行在于特征层面,在训练每颗树之前,对特征进行预排序,后续的并行迭代过程中重复使用这个排序结果,可以大大减少计算量,并提升模型性能。在查找最佳分裂点的时候,需要选择增益最大的特征取值作为分裂点,那么各个特征的增益计算就可以采用并行的方式进行计算,采用的是多线程方式计算各个特征的各个值得分裂增益。
结束语
OK,针对XGBoost的原理解析就此结束了,也算是给XGBoost一个交代吧。整篇文章花了不少时间在公式的勘误上面,不过在仔细检查每个公式的过程中,对XGBoost的公式推导又加深了好多遍,并且对公式的推导也有了更进一步的理解。其中有一点是比较突出的,很多人误认为XGBoost的增益是分裂后的减去分裂前,这是不正确的,其实是分裂前减去分裂后,可以通过公式计算出来。回头看看,XGBoost在工程实现上面也花了很大的心思,着实令人佩服,失敬失敬!接下来,将花点时间整理下Boosting的下一个模型:lightGBM。