Boosting模型：lightGBM 算法原理

Posted on   |   In   |     |   views

在上篇文章Boosting模型：XGBoost原理剖析一文中，详细介绍了陈天奇等人于2014年发布的XGBoost的内在原理，同时阐述了其特有的几大优点。然时代变化之迅速，新技术如春笋般应运而生，与日俱进。继xgboost之后，2016年微软进一步发布了GBDT的另一个实现：lightGBM。据悉，与XGBoost相比，在相同的运行时间下能够得到更好的预测性能。同时，在multi-class classification、click prediction和排序（learning to rank）都有很好的效果。本文将基于lightGBM的原始paper，对其原理进行归纳总结，以供后续参详，温习之用。

前言

为了确保文章的连续性，读者需对Boosting系列有一定的理解，在阅读本文核心内容之前，还读者预先在心里回答下下面几个问题：

  1. XGBoost的目标函数表达式？
  2. XGBoost在GBDT的基础上做了哪些优化？
  3. XGBoost的exact greedy Algorithm for split finding是什么？
  4. XGBoost寻找分裂点的增益计算方法？
  5. XGBoost的近似算法原理？
  6. 解释下Weighted Quantile Sketch原理？

如果对上面的问题模棱两可的，可前往上一篇文章:Boosting模型：XGBoost原理剖析，回顾一下。接下来将会针对XGBoost的不足进一步探讨lightGBM模型，相对于GBDT，lightGBM的精度与它相差不大，但是速度可以提升20倍。By the way，在学习lightGBM的时候，可以思考下下面几个问题（本文不会直接给出结论，读完之后，读者自然就明白了）：

  1. Adaboost、GBDT、XGBoost的样本梯度都是什么？
  2. XGBoost的不足之处在哪里（lightGBM因何诞生，解决了什么问题）？
  3. XGBoost的近似算法与lightGBM的histogram-based方法的区别？
  4. 什么是lightGBM？
  5. lightGBM与XGBoost的结构有什么区别？

不管是XGBoost还是lightGBM，模型的优化方向上必不可少的就是决策树的分裂上。下面，将重点介绍lightGBM算法在寻找最佳切分点上所做出的努力。

寻找最佳分裂点

lightGBM引入的核心思想包括两个方面：

  1. Histogram: 基于特征的数值进行分bin，然后基于bin的值寻找最佳分裂的bin值。
  2. GOSS(Gradient based One Side Sampling): 移除小梯度样本，使用余留的样本做增益计算；
  3. EFB(exclusive Feature Bundling)：bundle不会同时为零的特征（互斥），达到减少特征数量的目的。

Histogram分桶策略

GBDT是以决策树为基学习器的ensemble模型，在每次迭代中，GBDT都通过拟合负梯度来学习决策树，其中代价最大最耗时的就是寻找最佳切分点过程。一种方法是采用了预排序的算法，然后枚举所有可能的切分点，再寻找到增益最大的分裂点；另一中方法是基于histogram的算法，如下图所示。histogram算法并不是在预排序的特征值当中寻找最佳切分点，而是将连续的特征值进行离散化bin并放入不同的bucket，在训练的时候基于这些bin来构建特征histogram。这种做法效率更高，速度更快。如Algorithm 1所示，构建histogram的时间复杂度为O(#data $\times$ #feature)，寻找最佳分裂点的时间复杂度O(#bin $\times$ #feature)。

左侧为histogram分桶策略，右侧为GOSS采样方法

GOSS采样策略

样本的梯度越小，则样本的训练误差越小，表示样本已经训练的很好了。最直接的做法就是丢掉这部分样本，然而直接扔掉会影响数据的分布，因此lightGBM采用了one-side 采样的方式来适配：GOSS。GOSS保留了所有的大梯度样本，对小梯度样本进行随机采样，同时为了保证分布的一致性，在计算信息增益的时候，将采样的小梯度样本乘以一个常量：$\frac{1-a}{b}$，$a$表示Top $a \times 100\%$的大梯度样本比例值，$b$表示小梯度样本的采样比值（很多文章里面理解成从省下的小梯度样本中采样b%的比例，其实是有误解的，这里的百分比是相对于全部样本而言的，即$b \% \times N$）。例如：100个样本中，大梯度样本有20个，小梯度样本80个，小梯度样本量是大梯度样本数据量的$4$倍，则大样本采样比率$a$等于$0.2$，假设小梯度样本的采样率为$30\%$，则$b=0.3$，那么小梯度样本的采样数目等于$b \times 100=30$个，为了保证采样前后样本的分布保持一致，最后小梯度样本采样得到的数据在计算梯度时需要乘以$\frac{1-a}{b}=\frac{1-0.2}{0.3}=\frac{8}{3}$(解释一下，乘以$1-a$是因为大梯度样本采样的整体是整个样本集$N$，小梯度样本采样的候选样本集为$(1-a)N$，除以$b$是因为采样导致小梯度样本的整体分布减少，为此需要将权重放大$\frac{1}{b}$倍)。整个过程如上图Algorithm 2所示。

原始情况下，在第$j$个特征，值为$d$处进行分裂带来的增益可以定义为：

$$
V_{j|O}(d) = \frac{1}{n_O}\left(\frac{(\sum_{x_i\in O:x_{ij} \le d}g_i)^2}{n_{l|O}^j(d)} + \frac{(\sum_{x_i\in O:x_{ij} \gt d}g_i)^2}{n_{r|O}^j(d)} \right)
\tag{1}\label{1}
$$

其中O为在决策树待分裂节点的训练集，$n_o = \sum I(x_i \in O)$，$n_{l|O}^j(d) = \sum I[x_i \in O: x_{ij} \le d]\ $ 并且$\ n_{r|O}^j(d) = \sum I[x_i \in O: x_{ij} \gt d]$。

采用GOSS之后，分裂的增益可表示为为：

$$
V_{j|O}(d) = \frac{1}{n_O}\left(\frac{(\sum_{x_i\in A_l} g_i + \frac{1-a}{b} \sum_{x_i\in B_l} g_i)^2 }{n_{l}^j(d)} + \frac{(\sum_{x_i\in A_r} g_i + \frac{1-a}{b} \sum_{x_i\in B_l} g_r)^2 }{n_{r}^j(d)} \right)
\tag{2}\label{2}
$$

其中$A_l = {x_i \in A: x_{ij} \le d}, A_r = {x_i \in A: x_{ij} \gt d}$，$B_l = {x_i \in B: x_{ij} \le d}, B_r = {x_i \in B: x_{ij} \gt d}$.

EFB特征合并

高维数据通常是非常稀疏的，而且很多特征是互斥的（即两个或多个特征列不会同时为0），lightGBM对这类数据采用了名为EFB（exclusive feature bundling）的优化策略，将这些互斥特征分组合并为#bundle个维度。通过这种方式，可以将特征的维度降下来，相应的，构建histogram所耗费的时间复杂度也从O(#data $\times$ #feature)变为O(#data $\times$ #bundle)，其中#feature << #bundle。方法说起来虽然简单，但是实现起来将面临两大难点：

  1. 哪些特征可以bundle在一起；
  2. 如何构建bundle，实现特征降维。

针对这两个问题，paper里面提到了两种算法：Greedy Bundling和Merge Exclusive feature。

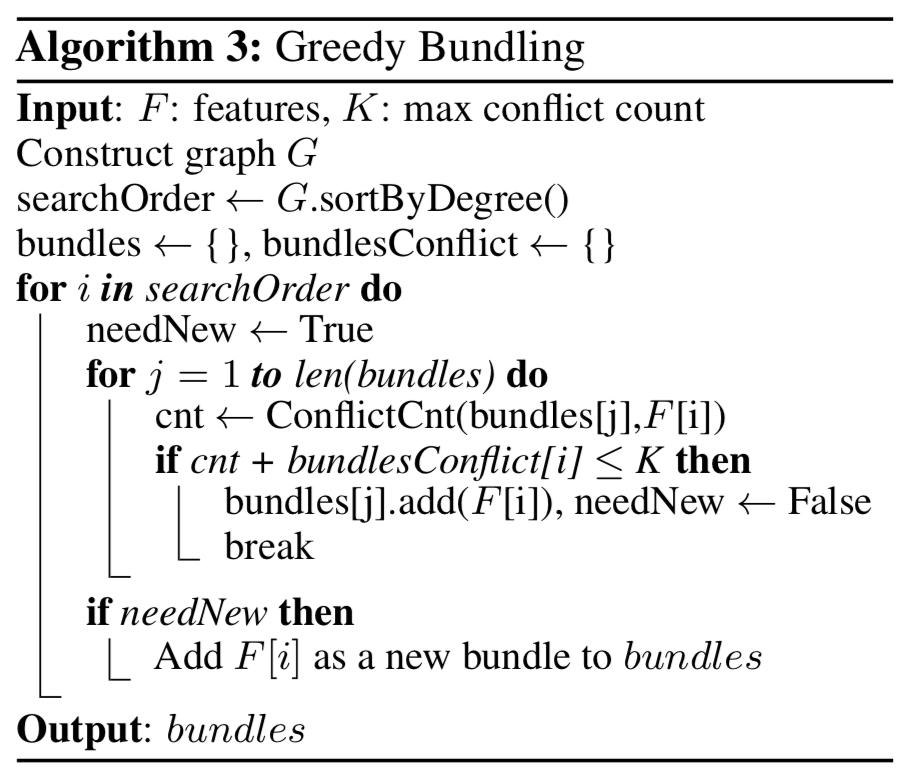
对于第一个问题，将特征划分为最少数量的Bundle本质上属于NP-hard problem。原理与图着色相同，给定一个图G，定点为$V$，表示特征，边为$E$，表示特征之间的互斥关系，接着采用贪心算法对图进行着色，以此来生成bundle。不过论文中指出，对于特征值得互斥在一定程度上是可以容忍的，具体的读者可以参考下原paper(文献1)。具体的算法流程如Algorithm 3所示。

  1. 首先构建一张带权重的图，权重为特征间的总冲突数；
  2. 对特征按照在图内的度进行降序排序；
  3. 检查排好序的特征，并将其划分到一个冲突较小的bundle里，如果没有就创建一个bundle。

采用这种方法对于特征数目不大的数据，还算OK，但是对于超大规模的特征将会出现性能瓶颈。一个优化的方向就是：采用非0值得个数作为排序的值，因为非零值越多通常冲突就越大。

对于第二个问题：应该如何如何构建bundle？关键在于构建前的特征的值在构建后的bundle中能够识别。由于基于histogram的方法存储的是离散的bin而不是连续的数值，因此我们可以将不同特征的bin值设定为不同的区间即可。例如，特征A的bin值为[0,10)，特征B的bin值为[0,20)，要想将两个特征bin合并，我们可以将特征B的特征bin的值加上10，其取值区间将变为[0,30)。整个方法描述如下图所示。

leaf-wise生长策略

另外，在树的生成方式上，lightGBM与XGBoost也是有区别的。lightGBM的生长策略是leaf-wise，XGBoost中决策树的生长策略是level-wise。对比之下，level-wise策略维持的是一颗平衡树，leaf-wise策略以降低模型损失最大化为目的，对当前level中切分增益最大的leaf节点进行切分。不过leaf-wise存在一个弊端，就是最后会得到一颗非常深的决策树，为了防止过拟合，可以在模型参数中设置决策树的深度。

左侧为level-wise（XGBoost），右侧为leaf-wise（lightGBM）

结束语

lightGBM主要提出了两个新颖的方法：GOSS和EFB。两者都对算法性能的提升有着重要的贡献，其中GOSS是针对分裂时样本的数目进行采样优化（行优化），EFB是针对特征进行合并，达到特征减少的目的（列优化）。实际上，XGBoost和lightGBM都属于GBDT的一种实现，旨在优化算法的性能，提升算法的训练速度，与XGBoost相比，lightGBM更适应于数据量更大的场景。从GBDT->XGBoost->lightGBM，在模型训练阶段，是不能百分百地断定lightGBM就比GBDT和XGBoost好，因为数据量的大小也决定了模型的可行性。所以实际场景中，还是建议一一尝试之后再做抉择，因为训练一个XGBoost或lightGBM，都是非常简单的事情。OK，基于Boosting模型的学习终于告一段落，后续将对基于深度学习的排序方法或CTR预估方法进行探讨，感谢读者耐心读完本文。

References

  1. Ke, Guolin, et al. “Lightgbm: A highly efficient gradient boosting decision tree.“ Advances in Neural Information Processing Systems. 2017.
  2. Chen, Tianqi, and Carlos Guestrin. “Xgboost: A scalable tree boosting system.“ Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining. ACM, 2016.
  3. LightGBM and XGBoost Explained
  4. xgboost docs
  5. lightGBM docs
  6. Boosting模型：XGBoost原理剖析
  7. Boosting模型：GBDT原理介绍
  8. XGBOOST vs LightGBM: Which algorithm wins the race