Deep Learning - CNN原理剖析

Posted on   |   In   |     |   views

在Deep Learning - 神经网络与BP算法一文中介绍了神经网络的原理，可以发现不同层之间是全连接的，当神经网络的深度、节点数变大，会导致过拟合、参数过多等问题。因此，本文将介绍另一种神经网络：CNN，卷积神经网络。

CNN简介

卷积神经网络通常是由三种层构成：卷积层，Pooling层（一般指Max Pooling）和全连接层（简称FC）。ReLU激活函数也应该算是是一层，它逐元素地进行激活函数操作。在本节中将讨论在卷积神经网络中这些层通常是如何组合在一起的。

一个典型的CNN框架

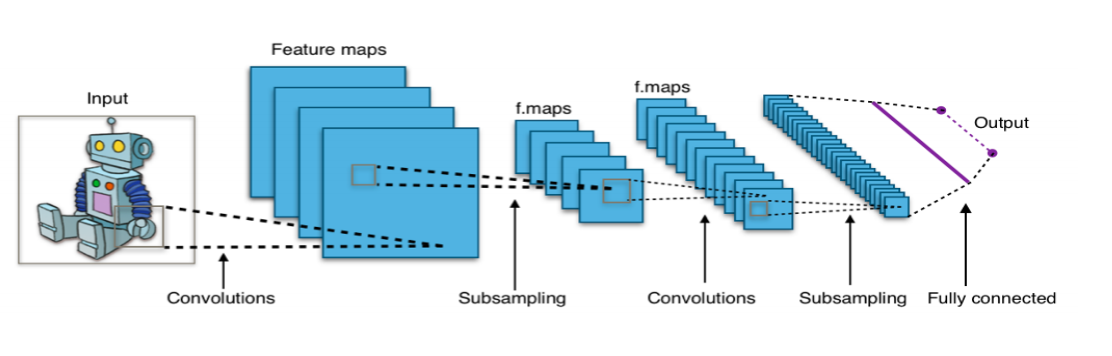
一个CNN网络由若干卷积层、Pooling层、全连接层组成。你可以构建各种不同的卷积神经网络，它的常用架构模式为：

INPUT -> [[CONV -> ReLU] * N -> POOL?]*M -> [FC -> RELU] * K -> FC

即N个[卷积层 + ReLU层]叠加，然后叠加一个可选的Pooling 层，整个结构重复M次，最后叠加K个[全连接+Relu]层。通常，

  • 当N = M = K = 0时，INPUT -> FC是一个线性分类；
  • INPUT -> CONV -> RELU -> FC
  • INPUT -> [CONV -> RELU -> POOL]*2 -> FC -> RELU -> FC。此处在每个Pooling 层之间有一个CONV层;
  • INPUT -> [CONV -> RELU -> CONV -> RELU -> POOL]*3 -> [FC -> RELU]*2 -> FC。此处每个Pooling层前有两个卷积层，这个思路适用于更大更深的网络，因为在执行具有破坏性的Pooling操作前，多重的卷积层可以从输入数据中学习到更多的复杂特征。

原理分析

下面对CNN的原理进行深层次剖析，当然，由于笔者能力有限，解释模糊的地方还望读者谅解。

对于卷积神经网络，主要有两个特性：

  1. 局部感知：卷积核；
  2. 局部权值共享：每个卷积过程的权重相同。

卷积神经网络的层次依次是输入层、卷积层、ReLU层、Pooling层、输出层，具体细节请往下看。

输入层

对于输入层，以图像为例，通常是一张图片的$n*n$的像素点，如果考虑RGB三种通道，输入就为$n*n*3$的图像。

卷积层

卷积层是CNN的核心层，它的作用是进行特征提取。卷积层若干卷积单元组成，卷积单元的参数都是通过反向传播算法最佳化得到的。在这一层，我们通过卷积核可以得到更深层次的feature map，每个卷积运算的目的都是为了提取输入图的不同特征，第一层卷积层可能是指提取一些低级的特征如边缘、线条和角等，更多层的网路能从低级特征中迭代提取更复杂的特征。

卷积层需要着重关注的几个点：

  • 局部感知（Local Connectivity）：卷积核（也叫滤波器，感受野）的大小；
  • 空间排列（Spatial arrangement）：卷积层的输出；
  • 参数共享（Parameter Sharing）：卷积核上的权重一样。

那么对于卷积层，怎么计算输出层的大小呢？请看下面：

  1. 首先接收一个$3D$的立体图像，长宽高表示为：$W_{1} \times H_{1} \times D_{1}$
  2. 超参数
    • filter卷积核的数量$K$;
    • 卷积核的大小$F$，例如$3*3$的卷积核，$F=3$;
    • 步长stride：$S$;
      • zero padding（零填充），补零数$P$，表达式为：$P = (F - 1)/2$;
  3. 输出一个新的3D对象：$W_{2}\times H_{2}\times D_{2}$，那么输出的图像各个维度的大小为：
    • $W_{2} = (W_{1} - F + 2P)/S + 1$;
    • $H_{2} = (H_{1} - F + 2P)/S + 1$;
    • $D_{2} = K$（卷积核的个数，对应输出层的深度）;
  4. 通过参数共享，每个filter共携带$F\cdot F \cdot D_{1}$个权值，对于整个卷积层，共有$(F\cdot F \cdot D_{1})\cdot K$个权值，另外还有$K$个偏置bias。

ReLU层

ReLU层就是激活函数层，这里把它单独出来是因为这一层充当非常重要的作用，它可以增强判定函数和整个神经网络的非线性特性，而本身并不会改变卷积层的空间排列。不同的激活函数产生的效果也大不相同，这里采用ReLU而不采用sigmoid或tanh的主要原因是ReLU可以克服vanishing gradient problem。ReLU的表达式如下：

$$
f(x) = max(0, x)
\tag{1} \label{1}
$$

使用ReLU的四个原因：

  1. fast to compute.
  2. biological reason.
  3. infinite sigmoid with different biases.
  4. vanising gradient problem.

关于第四点，CNN采用ReLU能够解决梯度消失问题，原理如下：假设经过第$i$层卷积之后，得到的输出为$f_i$，那么有:

$$
f_1 = f(w_1x + b_1) = f(net _ 1)
$$

$$f_2 = f(w_2f(w_1x + b_1) + b_2) = f(net _2)$$

$$f_3 = f(w_3f(w_2f(w_1x + b_1) + b_2) + b_3) = f(net _3)$$

假设最终损失为$L$，通过BP可以推导出：

$$
\frac{\partial L}{ \partial w_1} = \frac{\partial L}{ \partial f_3} \frac{\partial f_3}{ \partial net_3} w_3 \frac{\partial f_2}{ \partial net_2} w_2 \frac{\partial f_1}{ \partial net_1} \frac{\partial net_1}{ w_1}
\tag{2} \label{2}
$$

当$f$为sigmoid时，$\frac{\partial f_3}{ \partial net_3}$与$\frac{\partial f_2}{ \partial net_2}$均大于0，小于等于0.25（sigmoid激活函数的导数为$y * (1-y) \leq \frac{y^2 + (1-y)^2}{2} $，当且仅当 $y = 1-y$时取等号），所以当层数比较大的时候，就会出现“梯度消失”的问题。当激活函数为ReLU的时候，偏导数只在$0$和$1$两个数，所以只要在第一层中有一个不为零的偏导数，后面所有的偏导数均不为0。

Pooling层

Pooling层相当于采样层，通常有max pooling、average pooling、L2-norm pooling。

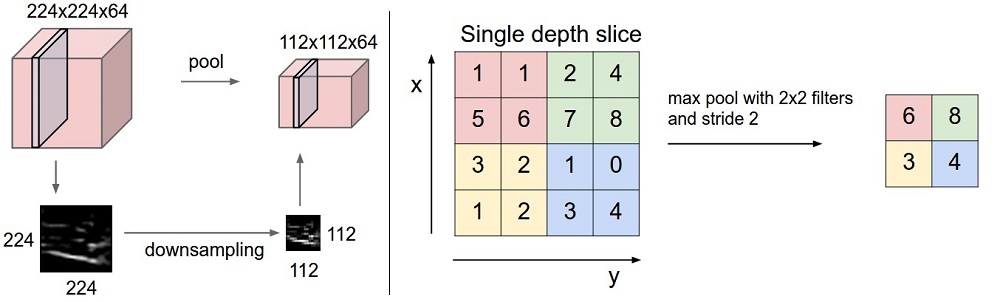
图片来自【[cs231n - cnn](http://cs231n.github.io/convolutional-networks/)】：Pooling层在空间上是对卷积层进行采样。图左：在本例中，大小为[224x224x64]的输入卷积层与大小为2的filter合并，步长为2最后输出图的大小为[112x112x64]。注意，变换前后深度是不变的。图右：最常见的降采样操作是max pooling，实例的步长为2。也就是说，每个max比较的元素为4个数字（2x2的方正）

那么经过pooling层之后，输出图的大小如何计算呢？请看下面：

  1. 接收一个3D的立体对象：$W_{1} \times H_{1} \times D_{1}$
  2. 必备超参数
    • filter的空间大小：$F$
    • 步长$S$
  3. 输出一个新的3D对象：$W_{2}\times H_{2}\times D_{2}$
    • $W_{2} = (W_{1} - F)/S + 1$
    • $H_{2} = (H_{1} - F)/S + 1$
    • $D_{2} = D_{1}$
  4. 将输入导入固定函数，引入0参数

FC层

FC层中的神经元与前一层中的所有激活具有完全连接，如在常规神经网络中所见。因此，它们的激活函数可以用一个矩阵乘法和一个偏移量来计算，即$wx+b$。同时，使用一个损失函数来“惩罚”网络的预测结果和真实结果之间的差异。例如，Softmax 交叉熵损失函数用于多分类问题，而Sigmoid交叉熵损失函数常常用于二分类问题。

权值更新推导

首先，回忆下上一篇文章神经网络和反向传播算法介绍的反向传播算法，整个算法分为三个步骤：

  1. 前向计算每个神经元的输出值；
  2. 反向传播计算每个神经元的误差项$\delta_{i}$，实际上是网络的损失函数$E_{k}$对神经元加权组成的网络的偏导数，即$\delta_i=\frac{\partial{E_k}}{\partial{net_i}}$；
  3. 计算神经元连接权重梯度$w_{ij}$（$w_{ij}$表示从神经元$j$连接到神经元$i$的权重），公式为$\frac{\partial{E_{k}}}{\partial{w_{ij}}}=\delta_{i}a_{j}$，其中，$a_{j}$表示神经元$j$的输出。然后根据梯度下降法则更新每个权重。

对于卷积神经网络，由于CONV和pooling下采样层的出现，影响了第二步$\delta$的计算，同时权值共享影响了第三步$w_{ji}$的更新。下面来详细分析卷积层和pooling层的反向传播过程，通过分析参数更新规则来进一步理解卷积神经网络。

对于卷积网络的权值推导，误差使用BP算法由后往前传递，可依次将其分为以下三部分：

  1. 输出层
  2. Pooling层
  3. 池化层

输出层是全连接层，其权值更新规则与上一篇文章介绍的一样，本文不再详细介绍。下面来看Pooling层与卷积层。

在公式推导之前，先对几个核心的变量进行简单说明，如下表：

变量 描述
$E_{total}$ 表示整个网络输出层的误差和
$\delta_{k}^{l}$ 表示第$l$层，第$k$个神经元的误差项
$a_{k}^{l}$ 表示第$l$层，第$k$个神经元的输出
$net_{k}^{l}$ 表示第$l$层，第$k$个神经元的输入
$w^{l}$ 表示第$l$层filter的权重
$f(net)$ f表示激活函数

Pooling Layers 池化层

克罗内克积(Kronecker product)

$$
\delta_k^{l-1} = \frac{\partial E_{total}}{\partial a_k^{l-1}} \frac{\partial a_k^{l-1}}{\partial net_k^{l-1}} = up(\delta_k^l) \odot f^{‘}(net_k^{l-1})
\tag{3} \label{3}
$$

其中，up函数表示上采样，完成了池化误差矩阵放大与误差重新分配的逻辑。

Convolution Layers 卷积层

前一层的feature map与卷积核进行卷积，然后输入到激活函数$f$中，形成输出层的feature map。每个输出图可由多个卷积核与多个输入图卷积加和而成。如下图：

整个卷积层的形式如下：

$$
a^{l}_{j} = f \left ( \sum_{i \in M_{j} } a_{i}^{l-1} \ast k_{ij}^{l} + b_{j}^{l} \right )
\tag{4} \label{4}
$$

其中$M_{j}$表示选择的输入图，$b$表示每个输出图携带的一个额外的偏置项。对于一个特定的输出图，卷积各个输入图的卷积核是不一样的。也就是说，如果输出feature map $j$和输出feature map $k$都是从输入图 $i$中卷积求和得到，那么两者对应的卷积核是不一样的。

在CNN反向传播过程中，假设输出层是是第$l+1$层，那么第$l$层是Pooling层，第$l-1$层属于卷积层。现在，输出层与Pooling层的误差项已经可以计算出来，现在，我们通过Pooling层的误差项$\delta_{l}$来推导卷积层的误差项$\delta^{l-1}$。

首先，$l$层与$l-1$层的输出值之间的关系如下：

$$
a^l= f(net^l) = f \left (a^{l-1}*W^l +b^l \right )
\tag{5} \label{5}
$$

下面，我们通过一个实例，来归纳卷积层的误差项$\delta^{l-1}$的计算式。

假设我们$l-1$层（卷积层）是一个$3 \times 3$的矩阵，filter是一个$2 \times 2$ 的矩阵，在步长为1，没有零填充的条件下，输出层（即$l$层）则是一个$2 \times 2$的矩阵。表达式可表示如下（输出层没有增加激活函数）：

$$
\left( \begin{array}{ccc} a_{11}^{l-1}&a_{12}^{l-1}&a_{13}^{l-1} \\
a_{21}^{l-1}&a_{22}^{l-1}&a_{23}^{l-1}\\
a_{31}^{l-1}&a_{32}^{l-1}&a_{33}^{l-1} \end{array} \right) * \left( \begin{array}{ccc} w_{11}^{l}&w_{12}^{l}\\
w_{21}^{l}&w_{22}^{l} \end{array} \right) = \left( \begin{array}{ccc} net_{11}^{l}&net_{12}^{l}\\
net_{21}^{l}&net_{22}^{l} \end{array} \right)
\tag{6} \label{6}
$$

通过卷积的定义，我们可以轻松得知各个$net$的表达式：

$$
net_{11}^{l} = a_{11}^{l-1}w_{11}^{l} + a_{12}^{l-1}w_{12}^{l} + a_{21}^{l-1}w_{21}^{l} + a_{22}^{l-1}w_{22}^{l} \\
net_{12}^{l} = a_{12}^{l-1}w_{11}^{l} + a_{13}^{l-1}w_{12}^{l} + a_{22}^{l-1}w_{21}^{l} + a_{23}^{l-1}w_{22}^{l} \\
net_{21}^{l} = a_{21}^{l-1}w_{11}^{l} + a_{22}^{l-1}w_{12}^{l} + a_{31}^{l-1}w_{21}^{l} + a_{32}^{l-1}w_{22}^{l} \\
net_{22}^{l} = a_{22}^{l-1}w_{11}^{l} + a_{23}^{l-1}w_{12}^{l} + a_{32}^{l-1}w_{21}^{l} + a_{33}^{l-1}w_{22}^{l}
\tag{7} \label{7}
$$

模拟反向求导，可得

$$
\nabla a^{l-1} = \frac{\partial E_{total}}{\partial a^{l-1}} = \frac{\partial E_{total}}{\partial net^{l}} \frac{\partial net^{l}}{\partial a^{l-1}} = \delta^{l} \frac{\partial net^{l}}{\partial a^{l-1}}
\tag{8} \label{8}
$$

根据上式，我们将各个偏导数展开，如下：

$$
\begin{align}
&\nabla a_{11}^{l-1} = \delta_{11}^{l}w_{11}^{l} \\
&\nabla a_{12}^{l-1} = \delta_{11}^{l}w_{12}^{l} + \delta_{12}^{l}w_{11}^{l}\\
&\nabla a_{13}^{l-1} = \delta_{12}^{l}w_{12}^{l} \\
&\nabla a_{21}^{l-1} = \delta_{11}^{l}w_{21}^{l} + \delta_{21}^{l}w_{11}^{l}\\
&\nabla a_{22}^{l-1} = \delta_{11}^{l}w_{22}^{l} + \delta_{12}^{l}w_{21}^{l} + \delta_{21}^{l}w_{12}^{l} + \delta_{22}^{l}w_{11}^{l} \\
&\nabla a_{23}^{l-1} = \delta_{12}^{l}w_{22}^{l} + \delta_{22}^{l}w_{12}^{l} \\
&\nabla a_{31}^{l-1} = \delta_{21}^{l}w_{21}^{l} \\
&\nabla a_{32}^{l-1} = \delta_{21}^{l}w_{22}^{l} + \delta_{22}^{l}w_{21}^{l} \\
&\nabla a_{33}^{l-1} = \delta_{22}^{l}w_{22}^{l}
\end{align}
\tag{9} \label{9}
$$

将上面的几个表达式用矩阵的形式转换，形式如下：

$$
\left( \begin{array}{ccc} 0&0&0&0 \\
0&\delta_{11}^{l}& \delta_{12}^{l}&0 \\
0&\delta_{21}^{l}&\delta_{22}^{l}&0 \\
0&0&0&0 \end{array} \right) * \left( \begin{array}{ccc} w_{22}^{l}&w_{21}^{l}\\
w_{12}^{l}&w_{11}^{l} \end{array} \right)
= \left( \begin{array}{ccc} \nabla a_{11}^{l-1}&\nabla a_{12}^{l-1}&\nabla a_{13}^{l-1} \\
\nabla a_{21}^{l-1}&\nabla a_{22}^{l-1}&\nabla a_{23}^{l-1}\\
\nabla a_{31}^{l-1}&\nabla a_{32}^{l-1}&\nabla a_{33}^{l-1}
\end{array} \right)
\tag{10} \label{10}
$$

为了符合梯度计算，我们在误差矩阵周围填充了一圈0，此时我们将卷积核翻转后和反向传播的梯度误差进行卷积，就得到了前一次的梯度误差。

由于

$$
net^{l}=a^{l-1} \ast W^{l}+b^{l}=f(net^{l-1}) \ast W^{l}+b^{l}
\tag{11} \label{11}
$$

可以得知

$$
\begin{align}
\delta^{l-1}
&=\frac{ \partial E_{total}}{\partial net^{l-1}}\\
&=\frac{ \partial E_{total}}{\partial net^{l}} \frac{ \partial net^{l}}{ \partial net^{l-1}} \\
&= \color{ blue }{\frac{ \partial E_{total}}{\partial net^{l}} \frac{ \partial net^{l}}{ \partial a^{l-1}} } \color{red}{ \frac{ \partial a^{l-1}}{ \partial net^{l-1}}} \\
&= \color{blue} {\delta^{l}*rot180(W^{l})} \odot \color{red} {f^{‘}(net^{l-1})}
\end{align}
\tag{12} \label{12}
$$

上面分析的是误差项的传递，接下来计算误差对权值和偏置的偏导数。

$$
\begin{align}
\frac{ \partial E}{\partial W^{l}}
=\frac{ \partial E}{\partial net^{l}} \frac{ \partial net^{l}}{ \partial W^{l}}
=\delta^{l} \frac{ \partial net^{l}}{ \partial W^{l}}
= \color{blue} {\delta^{l}*rot180(a^{l-1})}
\end{align}
\tag{13} \label{13}
$$

对于权值的初始化，通常有下面三种选择：

  • 全0初始化（Bad）；
  • 比较小的随机数（Bad）；
  • 使用高斯分布来初始化，标准差为sqrt(2/n)，其中n为输出神经元的数量（Good）

Conclusion

CNN是人工神经网络的一种，人工神经网络里是用BP算法将误差层层回传，利用梯度下降更新每一层的权值，CNN中也是类似，主要是掌握BP算法。OK，关于CNN的总结暂且至此吧，推导部分的公式有点复杂，敲起来很不容易，有的地方也许存在误差，后续再进行修缮！下一篇开始RNN系列学习。

参考资料